What is the definition of modulo? - Entdecke die Welt der Modulo-Rechnung
Stell dir vor, du hast eine Uhr mit nur 12 Stunden. Es ist jetzt 14 Uhr. Wie würdest du die Uhrzeit auf dieser Uhr einstellen? Genau, du würdest 2 Uhr einstellen! Du hast soeben unbewusst die Modulo-Rechnung angewendet.
Klingt erstmal kompliziert? Keine Sorge, ist es aber gar nicht. Im Prinzip geht es bei der Modulo-Rechnung, oft auch einfach "Modulo" genannt, darum, den Rest einer Division zu berechnen. Klingt immer noch kompliziert? Okay, dann stell dir vor, du teilst 14 durch 12. Du erhältst 1 mit einem Rest von 2. Dieser Rest, die 2, ist genau das, was uns bei der Modulo-Rechnung interessiert. Man schreibt das dann so: 14 modulo 12 = 2.
Die Modulo-Rechnung ist ein grundlegendes Konzept in der Mathematik und Informatik und hat eine lange Geschichte. Sie wird schon seit der Antike verwendet, um zum Beispiel Kalenderberechnungen durchzuführen. Heute findet man sie in vielen Bereichen wieder, von der Kryptographie bis hin zur Programmierung.
Aber was macht die Modulo-Rechnung so besonders? Nun, sie erlaubt es uns, mit Zahlen in einem zyklischen System zu arbeiten, wie zum Beispiel bei unserer Uhr. Stellen wir uns vor, wir wollen wissen, welcher Wochentag in 100 Tagen sein wird. Anstatt mühsam 100 Tage zu zählen, können wir einfach 100 modulo 7 rechnen (da eine Woche 7 Tage hat). Das Ergebnis, in diesem Fall 2, sagt uns, dass es in 100 Tagen zwei Tage später als heute sein wird.
Die Modulo-Rechnung ist also ein mächtiges Werkzeug, das uns hilft, komplexe mathematische Probleme auf einfache und elegante Weise zu lösen. In den folgenden Abschnitten werden wir uns die Definition, Anwendungen und Vorteile der Modulo-Rechnung genauer ansehen.
Vorteile der Modulo-Rechnung
Die Modulo-Rechnung bringt einige Vorteile mit sich:
- Vereinfachung von Berechnungen: Komplexe mathematische Probleme, insbesondere bei der Arbeit mit großen Zahlen, lassen sich mithilfe der Modulo-Rechnung oft vereinfachen.
- Zyklische Daten: Die Modulo-Rechnung eignet sich hervorragend für die Arbeit mit zyklischen Daten, wie Wochentagen, Uhrzeiten oder Winkeln.
- Fehlererkennung: In der Informatik wird die Modulo-Rechnung häufig zur Fehlererkennung eingesetzt, z. B. bei der Überprüfung von Kreditkartennummern.
Beispiele für die Modulo-Rechnung
Hier sind einige Beispiele, die die Vielseitigkeit der Modulo-Rechnung demonstrieren:
- Berechnung des Wochentags: Wie bereits erwähnt, kann die Modulo-Rechnung verwendet werden, um den Wochentag in einer bestimmten Anzahl von Tagen zu bestimmen. Wenn heute Montag ist und wir wissen wollen, welcher Wochentag in 10 Tagen sein wird, berechnen wir einfach 10 modulo 7 = 3. Da Montag der erste Tag der Woche ist, ist der dritte Tag der Woche Mittwoch. Daher ist in 10 Tagen Mittwoch.
- Uhrenarithmetik: Stellen Sie sich eine Uhr mit 12 Stunden vor. Wenn es jetzt 8 Uhr ist und wir 5 Stunden hinzufügen, berechnen wir 13 modulo 12 = 1. Daher zeigt die Uhr 1 Uhr an.
- Kryptographie: Die Modulo-Rechnung spielt eine wichtige Rolle bei der Kryptographie, insbesondere bei der Erzeugung von Schlüsseln und der Verschlüsselung von Daten. Ein Beispiel hierfür ist der RSA-Algorithmus.
Tipps und Tricks zur Modulo-Rechnung
Obwohl die Modulo-Rechnung ein relativ einfaches Konzept ist, gibt es einige Tipps und Tricks, die Ihnen helfen können, sie besser zu verstehen und anzuwenden:
- Verwenden Sie einen Taschenrechner: Für einfache Berechnungen können Sie einen Taschenrechner verwenden. Die meisten Taschenrechner haben eine Modulo-Funktion, die normalerweise mit "mod" oder "%" gekennzeichnet ist.
- Übung macht den Meister: Wie bei jedem mathematischen Konzept ist Übung der Schlüssel zum Erfolg. Üben Sie die Modulo-Rechnung mit verschiedenen Zahlen und Szenarien, um Ihr Verständnis zu verbessern.
Fazit
Die Modulo-Rechnung mag auf den ersten Blick einschüchternd wirken, ist aber in Wirklichkeit ein einfaches und äußerst nützliches Werkzeug. Sie ermöglicht es uns, mit zyklischen Daten zu arbeiten, komplexe mathematische Probleme zu vereinfachen und sogar Daten zu verschlüsseln. Vom einfachen Bestimmen des Wochentags bis hin zur komplexen Kryptographie - die Anwendungen der Modulo-Rechnung sind vielfältig. Indem wir die Grundlagen der Modulo-Rechnung verstehen, können wir unsere Problemlösungsfähigkeiten verbessern und die Welt um uns herum besser verstehen.

Colorful frost fox in high definition on Craiyon | Taqueria Autentica

Illustration depicting warp points definition on Craiyon | Taqueria Autentica

Modulo Operation Definition (Illustrated Mathematics Dictionary) | Taqueria Autentica

Labyrinth of minerals in high definition on Craiyon | Taqueria Autentica
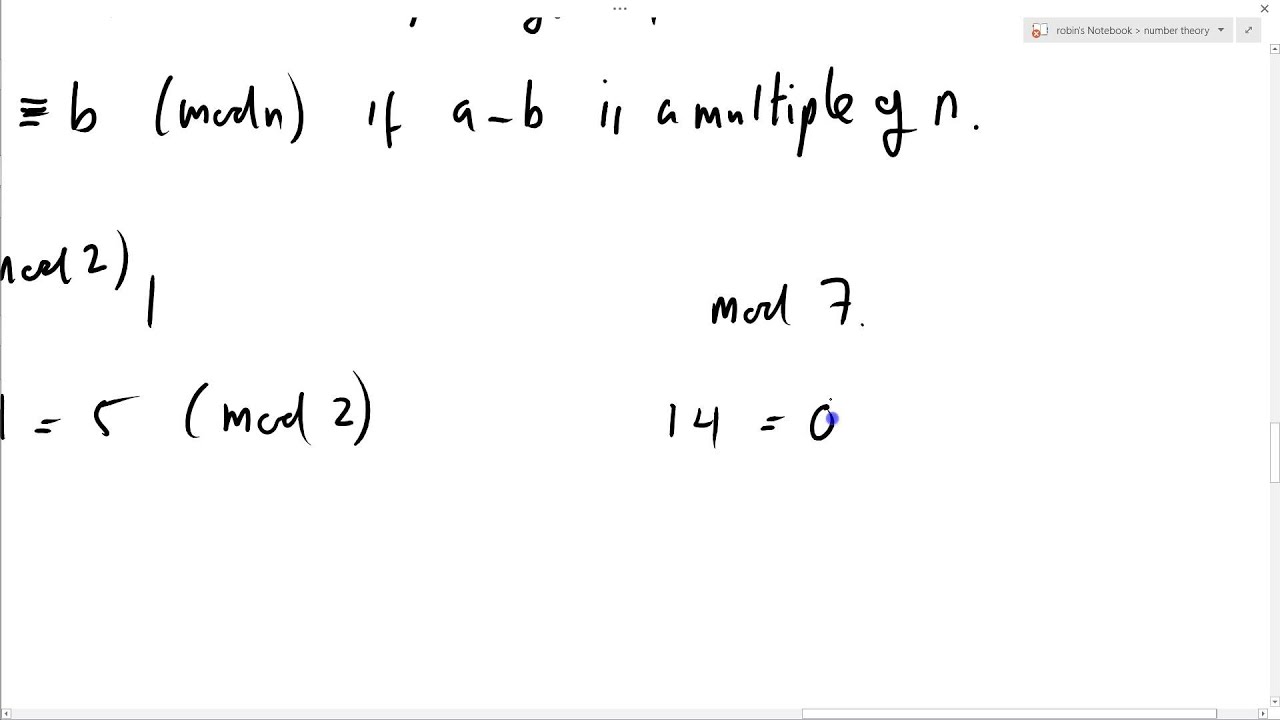
what is the definition of modulo | Taqueria Autentica

Hyper realistic high definition artwork on Craiyon | Taqueria Autentica

High definition fragmented leaf artwork on Craiyon | Taqueria Autentica

Portrait of a rajasthani young woman in high definition on Craiyon | Taqueria Autentica

Delicious cupcake in high definition on Craiyon | Taqueria Autentica

Trippy high definition environment on Craiyon | Taqueria Autentica

Vibrant and colorful high definition background on Craiyon | Taqueria Autentica

Solved 1. (3 pts) Use the definition of congruence modulo n | Taqueria Autentica

what is the definition of modulo | Taqueria Autentica

7 Pics Floored Quotient Definition And Description | Taqueria Autentica

Crystal clear water in high definition on Craiyon | Taqueria Autentica