El enigma matemático: Dividir cero entre cero
¿Qué ocurre si pulsamos el botón de dividir en una calculadora y luego introducimos cero, seguido de otro cero? Probablemente, la pantalla parpadee con un mensaje de error, quizás un lacónico "Math Error" o un más descriptivo "No se puede dividir entre cero". Este pequeño experimento, que a muchos nos ha picado la curiosidad en algún momento, nos lleva de cabeza a uno de los conceptos más fascinantes y problemáticos de las matemáticas: la división por cero, y más específicamente, el enigma de dividir cero entre cero.
En el mundo de las matemáticas, donde las reglas se rigen con precisión milimétrica, dividir por cero es como intentar cruzar la línea de meta en una carrera donde la meta simplemente no existe. Es un concepto que desafía la lógica y que ha intrigado a matemáticos durante siglos. La razón es sencilla: dividir significa repartir algo en partes iguales, pero ¿cómo podemos repartir algo en cero partes? La pregunta misma parece absurda.
Pero adentrémonos en el corazón de este enigma matemático. Mientras que dividir cualquier número por cero es problemático, dividir cero entre cero nos lleva a un nivel completamente nuevo de complejidad. Aquí, la intuición nos juega una mala pasada. Si dividimos cero manzanas entre cero personas, ¿no tendría sentido decir que cada persona recibe cero manzanas? A primera vista, parece lógico, pero aquí es donde la lógica matemática nos detiene en seco.
La respuesta, y agárrense fuerte, es que dividir cero entre cero es un resultado indefinido. Esto significa que no hay una respuesta única y válida. Imaginen una ecuación como 0/0 = x. Podríamos pensar que x = 0, pero también podríamos argumentar que x = 1, o x = cualquier otro número. Todas estas respuestas son igual de válidas y, al mismo tiempo, ninguna de ellas lo es.
Este carácter indefinido de dividir cero entre cero proviene de la forma en que las matemáticas definen la división. La división no es más que la operación inversa a la multiplicación. Por lo tanto, si decimos que 0/0 = x, entonces, según la definición de división, deberíamos tener 0 * x = 0. Pero aquí está el problema: cualquier número multiplicado por cero da como resultado cero. Es decir, cualquier valor de x satisfaría la ecuación, haciendo imposible determinar un valor único para x.
El debate sobre dividir cero entre cero ha trascendido las aulas y las pizarras. Filósofos y lógicos también han socinado sobre este concepto, explorando sus implicaciones en la naturaleza del infinito, el vacío y la propia realidad. ¿Acaso la imposibilidad de definir 0/0 apunta a una limitación fundamental de nuestro sistema numérico? ¿O es un recordatorio de que, a veces, las respuestas más sencillas son las más escurridizas?
En la práctica, la imposibilidad de dividir por cero tiene implicaciones en la computación y en el desarrollo de software. Los programadores deben tener en cuenta esta singularidad matemática para evitar errores fatales en sus programas. De hecho, muchos lenguajes de programación lanzan excepciones o errores cuando se intenta realizar esta operación.
En definitiva, aunque a simple vista pueda parecer un juego matemático trivial, el concepto de dividir cero entre cero nos lleva a un viaje fascinante por los límites de la lógica y el razonamiento. Nos obliga a cuestionar nuestras suposiciones básicas sobre los números y las operaciones matemáticas, y nos recuerda que incluso en un mundo aparentemente ordenado y predecible como el de las matemáticas, existen misterios que desafían nuestra comprensión.
Ventajas y Desventajas de considerar dividir cero entre cero
| Ventajas | Desventajas |
|---|---|
| Podría simplificar algunas ecuaciones matemáticas si se define de manera consistente. | Rompe las reglas fundamentales de la aritmética, llevando a contradicciones. |
| Podría tener aplicaciones en áreas de la física teórica que lidian con el infinito. | Crea ambigüedad en cálculos y modelos matemáticos. |
Aunque la matemática tradicional nos dice que dividir cero entre cero es imposible, el debate continúa. Algunos matemáticos exploran sistemas numéricos alternativos donde esta operación podría tener sentido. Sin embargo, hasta que no se llegue a un consenso, la división por cero, y en particular, dividir cero entre cero, seguirá siendo un enigma sin resolver, una paradoja que nos recuerda la complejidad y la belleza, a veces frustrante, del mundo matemático.

dividir cero entre cero | Taqueria Autentica

Understanding Zero Division: Indeterminacy in Mathematics | Taqueria Autentica

¿Se puede dividir entre 0? ¿El resultado es infinito? | Taqueria Autentica

Como evitar en Excel #¡DIV/0! al dividir entre cero | Taqueria Autentica

¿Cuánto es $40,000 dólares en pesos? | Taqueria Autentica

Twitter: La curiosa respuesta de Siri al dividir cero entre cero [VIDEO | Taqueria Autentica

¿Qué pasa cuando le pides a Siri dividir cero entre cero? | Taqueria Autentica

¿Se puede dividir entre 0? ¿El resultado es infinito? | Taqueria Autentica

Por qué no se puede dividir entre cero / Ideas En 5 Minutos | Taqueria Autentica

dividir cero entre cero | Taqueria Autentica
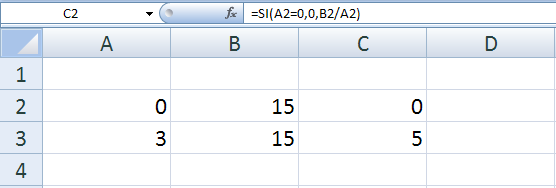
Capacitate Excel: Como evitar en Excel #¡DIV/0! al dividir entre cero | Taqueria Autentica

¿Dividir entre 0 da infinito? | Taqueria Autentica

¿Dividir entre 0 da infinito? | Taqueria Autentica

¿Se puede dividir entre 0? ¿El resultado es infinito? | Taqueria Autentica
Ley de los signos | Taqueria Autentica