¿Qué es el valor promedio y cómo puede ayudarte a entender el mundo?
Vivimos en un mundo inundado de datos. Desde las estadísticas deportivas hasta las finanzas, pasando por las calificaciones de productos, constantemente nos bombardean con números. ¿Pero cómo podemos dar sentido a toda esta información? Aquí es donde entra en juego el valor promedio.
El valor promedio, también conocido como media aritmética, es una herramienta fundamental para comprender y analizar datos. Nos permite resumir un conjunto de valores en un solo número que representa el centro de la distribución. Ya sea que estemos hablando de la altura de los estudiantes en una clase, el precio promedio de la gasolina o la temperatura media en un mes determinado, el valor promedio nos proporciona una idea general de lo que está sucediendo.
Pero el valor promedio no se limita solo a las matemáticas. Es una herramienta poderosa que se utiliza en una amplia gama de disciplinas, desde la ciencia y la ingeniería hasta la economía y las ciencias sociales. Nos ayuda a identificar tendencias, hacer comparaciones y tomar decisiones informadas.
A pesar de su aparente simplicidad, el valor promedio es un concepto con una rica historia y un impacto significativo en nuestra comprensión del mundo. Desde los primeros astrónomos que usaban promedios para calcular las órbitas de los planetas hasta los científicos modernos que los utilizan para analizar datos complejos, el valor promedio ha sido una constante en la búsqueda del conocimiento humano.
En este artículo, profundizaremos en el mundo del valor promedio. Exploraremos su definición, historia, importancia, los principales problemas relacionados con su uso, ejemplos prácticos, beneficios y mucho más. Al final de este viaje, comprenderás mejor cómo el valor promedio puede ayudarte a navegar por el mundo de los datos y a tomar decisiones más informadas.
Ventajas y Desventajas del Valor Promedio
Como cualquier herramienta estadística, el valor promedio tiene sus fortalezas y debilidades. Es importante ser conscientes de ambos aspectos para utilizarlo de manera efectiva y evitar interpretaciones erróneas.
| Ventajas | Desventajas |
|---|---|
| Fácil de calcular e interpretar | Sensible a valores atípicos (outliers) |
| Proporciona una medida representativa del centro de los datos | No siempre refleja la realidad de la distribución completa |
| Útil para comparar diferentes conjuntos de datos | Puede ser engañoso si se utiliza de forma aislada |
5 Mejores Prácticas al Utilizar el Valor Promedio
Para aprovechar al máximo el valor promedio y evitar posibles errores, aquí hay cinco consejos prácticos:
- Considera el contexto: El valor promedio por sí solo no cuenta toda la historia. Siempre analiza el contexto de los datos, incluyendo la fuente, el tamaño de la muestra y la variabilidad.
- Identifica valores atípicos: Los valores extremos pueden distorsionar el valor promedio. Identifícalos y decide si debes incluirlos o excluirlos del análisis.
- Utiliza otras medidas estadísticas: Combina el valor promedio con otras medidas como la mediana, la moda y la desviación estándar para obtener una imagen más completa de los datos.
- Visualiza los datos: Utiliza gráficos y diagramas para visualizar la distribución de los datos y detectar patrones que el valor promedio podría ocultar.
- Interpreta con precaución: Recuerda que el valor promedio es solo una herramienta. No saques conclusiones precipitadas basándote únicamente en este valor.
8 Preguntas Frecuentes sobre el Valor Promedio
A continuación, respondemos a algunas de las preguntas más comunes sobre el valor promedio:
- ¿Cuál es la diferencia entre valor promedio, mediana y moda? El valor promedio es la suma de todos los valores dividida entre el número total de valores. La mediana es el valor que se encuentra en el centro de un conjunto de datos ordenados. La moda es el valor que aparece con mayor frecuencia.
- ¿Cuándo es mejor utilizar el valor promedio, la mediana o la moda? La elección depende del tipo de datos y del objetivo del análisis. El valor promedio es útil para datos simétricos sin valores atípicos. La mediana es más robusta a valores atípicos. La moda es útil para datos categóricos.
- ¿Cómo se calcula el valor promedio ponderado? Se multiplica cada valor por su peso correspondiente, se suman los resultados y se divide entre la suma de los pesos.
- ¿Cómo afecta la dispersión de los datos al valor promedio? Una mayor dispersión de los datos implica que el valor promedio es menos representativo del conjunto de datos.
- ¿Cómo se interpreta un valor promedio alto o bajo? Un valor promedio alto o bajo debe interpretarse en relación con el contexto de los datos. Un valor promedio alto no siempre es positivo, y un valor promedio bajo no siempre es negativo.
- ¿Cuáles son las limitaciones del valor promedio? El valor promedio puede ser sensible a valores atípicos y no siempre refleja la realidad de la distribución completa de los datos.
- ¿Cómo puedo utilizar el valor promedio en la vida real? El valor promedio se puede utilizar para comparar precios, analizar el rendimiento académico, tomar decisiones financieras y mucho más.
- ¿Dónde puedo aprender más sobre el valor promedio y otras medidas estadísticas? Hay muchos recursos disponibles en línea y en bibliotecas sobre estadística básica y análisis de datos.
Conclusión: El poder del promedio en la era de la información
El valor promedio, a pesar de su aparente simplicidad, es una herramienta fundamental para dar sentido al mundo que nos rodea. Su capacidad para resumir información compleja en un solo número lo convierte en un aliado invaluable en la toma de decisiones, la identificación de tendencias y la comprensión de fenómenos complejos. Sin embargo, es crucial recordar que el valor promedio no es una panacea. Su uso efectivo requiere un análisis cuidadoso del contexto, la consideración de otras medidas estadísticas y una interpretación prudente de los resultados. Al dominar el arte del promedio, estaremos mejor equipados para navegar por el diluvio de información que caracteriza a la era digital y tomar decisiones más informadas en todos los aspectos de nuestras vidas.
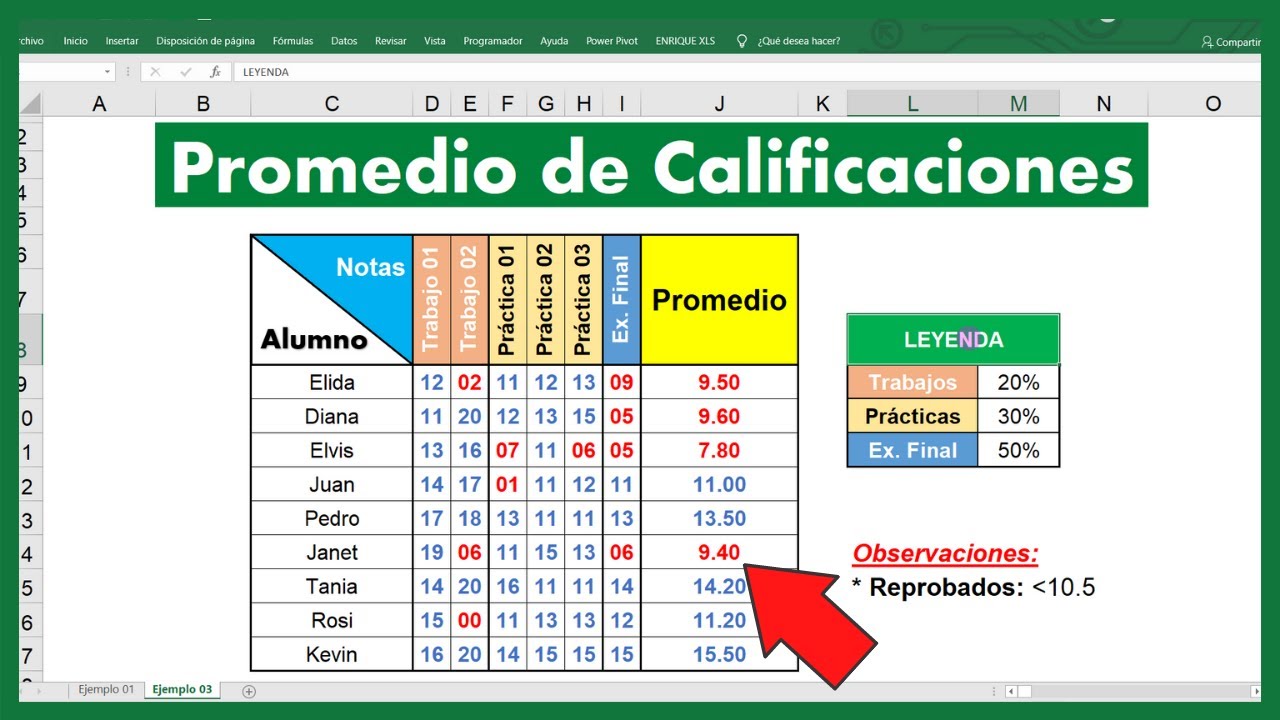
Calcular Promedio De Notas Con Diferentes Porcentajes En Excel | Taqueria Autentica

Valor promedio del voltaje | Taqueria Autentica

Como Calcular El Promedio Ponderado | Taqueria Autentica

Como Sacar La Media Aritmetica En Datos No Agrupados | Taqueria Autentica

Como Calcular El Promedio De Calificaciones | Taqueria Autentica
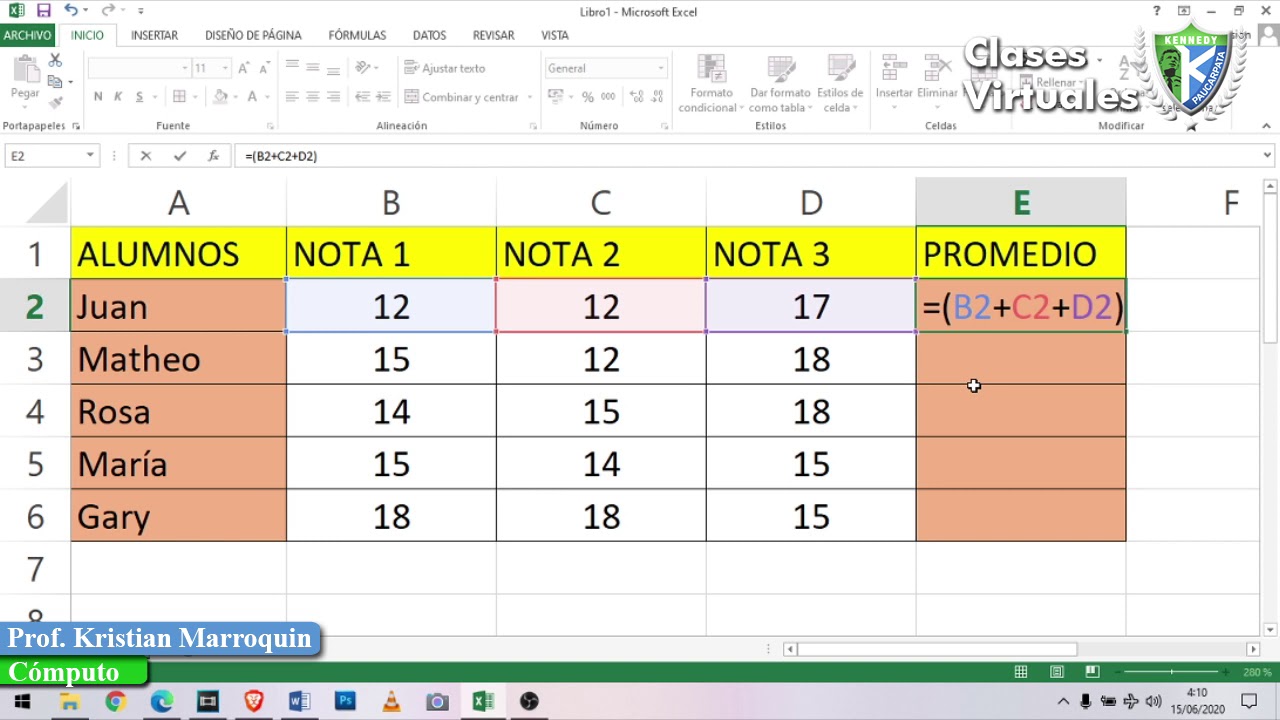
Formula De Promedio En Excel | Taqueria Autentica

Como Sacar El Promedio En Excel De Una Columna | Taqueria Autentica

Simbolo De Media Aritmetica | Taqueria Autentica

Como Se Calcula Un Promedio Ponderado En Excel | Taqueria Autentica

Calcule El Voltaje Promedio Con Esta Sencilla Fórmula | Taqueria Autentica

Como Calcular El Promedio De Una Columna En Excel | Taqueria Autentica

El símbolo de promedio en Excel: Cómo usar la fórmula AVERAGE para | Taqueria Autentica

zona Limpia el cuarto polilla como calcular potencia media esfera | Taqueria Autentica

Como Calcular El Promedio En Datos Agrupados | Taqueria Autentica
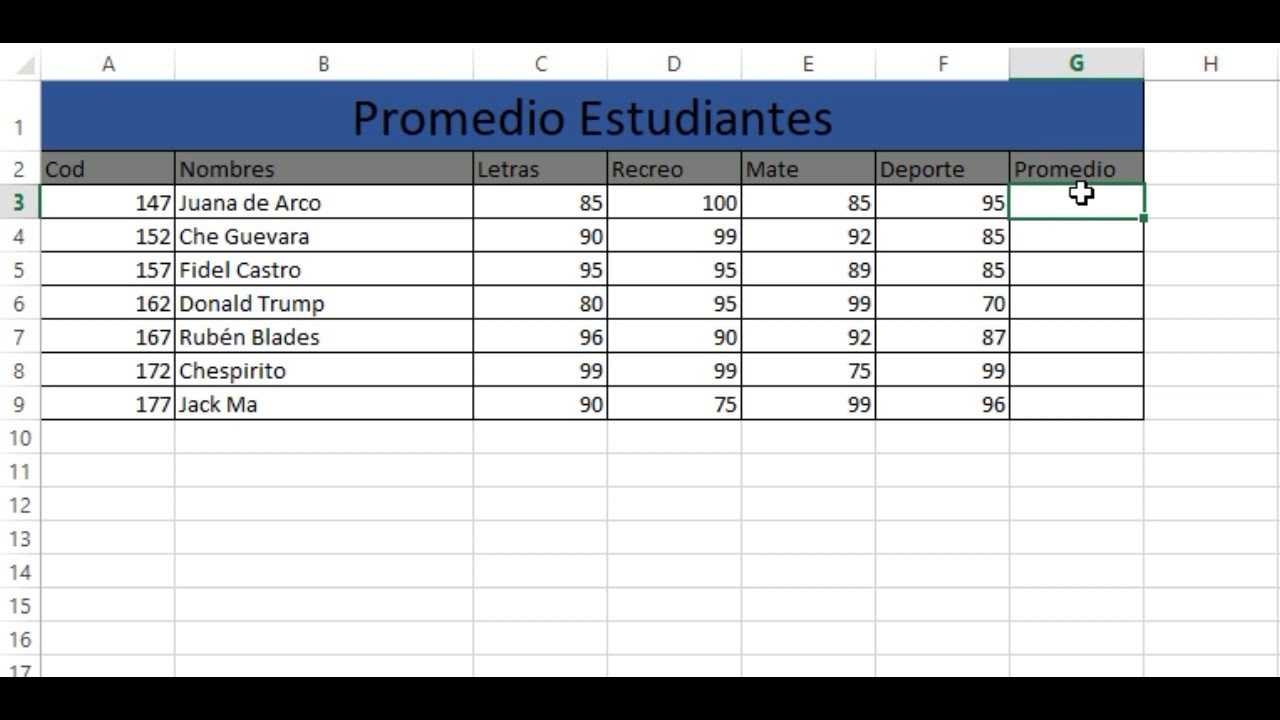
Como Sacar El Promedio De Varias Filas En Excel | Taqueria Autentica