Fungsi Matematik: Rahsia Gadget Ajaib!
Pernahkah anda terfikir bagaimana telefon pintar anda boleh memproses jutaan arahan dalam sekelip mata? Atau bagaimana kereta autonomus boleh menavigasi jalan raya dengan begitu tepat? Jawapannya terletak pada satu konsep matematik yang sangat penting: fungsi.
Fungsi, dalam dunia matematik, boleh dibayangkan sebagai 'kotak ajaib' yang memproses input dan menghasilkan output berdasarkan peraturan tertentu. Sama seperti mesin layan diri yang mengeluarkan minuman berdasarkan butang yang anda tekan, fungsi matematik juga beroperasi berdasarkan peraturan yang ditetapkan.
Konsep fungsi ini mungkin kelihatan abstrak pada mulanya, tetapi ia sebenarnya merupakan tulang belakang kepada banyak teknologi moden. Daripada algoritma carian Google hinggalah kepada sistem pengenalan wajah, fungsi matematik memainkan peranan yang sangat penting.
Sejarah fungsi matematik boleh dikesan kembali ke zaman Babylonia dan Mesir kuno, di mana ahli matematik menggunakan jadual untuk mewakili hubungan antara nombor. Namun, konsep fungsi yang lebih formal mula berkembang pada abad ke-17, dengan sumbangan daripada ahli matematik terkemuka seperti René Descartes dan Gottfried Wilhelm Leibniz.
Salah satu masalah utama yang mendorong perkembangan konsep fungsi adalah keperluan untuk memodelkan fenomena dunia sebenar secara matematik. Sebagai contoh, ahli fizik memerlukan fungsi untuk menggambarkan pergerakan objek, manakala ahli ekonomi memerlukan fungsi untuk memodelkan pertumbuhan ekonomi.
Secara ringkasnya, fungsi adalah konsep matematik yang sangat penting dengan aplikasi yang luas dalam pelbagai bidang. Memahami fungsi matematik bukan sahaja membuka pintu kepada dunia matematik yang lebih luas, tetapi juga membolehkan kita menghargai dengan lebih mendalam keajaiban teknologi yang kita gunakan setiap hari.
Kelebihan dan Kekurangan Fungsi Matematik
| Kelebihan | Kekurangan |
|---|---|
| Memudahkan pemodelan fenomena dunia sebenar. | Boleh menjadi kompleks dan sukar difahami bagi sesetengah pelajar. |
| Membolehkan analisis dan ramalan yang tepat. | Mungkin tidak selalu mencerminkan kerumitan situasi dunia sebenar. |
| Merupakan asas kepada banyak bidang sains dan teknologi. | Memerlukan pemahaman yang kukuh tentang konsep matematik asas. |
5 Amalan Terbaik untuk Memahami Fungsi Matematik
- Kuasai Asas: Pastikan anda memahami konsep asas algebra, seperti pembolehubah, persamaan, dan ketaksamaan.
- Visualisasikan Fungsi: Gunakan graf untuk menggambarkan hubungan antara input dan output fungsi. Ini akan membantu anda memahami tingkah laku fungsi dengan lebih baik.
- Latih Tubi: Selesaikan pelbagai masalah latihan yang melibatkan fungsi. Semakin banyak anda berlatih, semakin selesa anda dengan konsep ini.
- Cari Aplikasi Dunia Sebenar: Cuba kaitkan konsep fungsi dengan situasi dunia sebenar, seperti pergerakan objek atau pertumbuhan penduduk. Ini akan menjadikan pembelajaran lebih menarik dan relevan.
- Jangan Takut untuk Bertanya: Jika anda menghadapi masalah, jangan takut untuk bertanya kepada guru, pensyarah, atau rakan sekelas anda.
5 Contoh Nyata Fungsi Matematik
- Pergerakan Projektil: Fungsi boleh digunakan untuk memodelkan trajektori bola yang dilambung ke udara.
- Pertumbuhan Penduduk: Fungsi eksponen boleh digunakan untuk memodelkan pertumbuhan populasi bakteria atau manusia.
- Kecerunan Jalan: Fungsi linear boleh digunakan untuk mewakili kecerunan jalan raya.
- Suhu Badan: Fungsi trigonometri boleh digunakan untuk memodelkan perubahan suhu badan manusia sepanjang hari.
- Harga Saham: Fungsi boleh digunakan untuk menganalisis dan meramalkan turun naik harga saham.
5 Cabaran dan Penyelesaian Berkaitan Fungsi Matematik
- Cabaran: Memahami konsep domain dan julat fungsi. Penyelesaian: Visualisasikan fungsi pada graf dan kenal pasti nilai input (domain) dan output (julat) yang dibenarkan.
- Cabaran: Menentukan sama ada suatu hubungan adalah fungsi atau bukan. Penyelesaian: Gunakan ujian garis menegak. Jika sebarang garis menegak memotong graf lebih daripada sekali, maka hubungan tersebut bukanlah fungsi.
- Cabaran: Menyelesaikan persamaan dan ketaksamaan yang melibatkan fungsi. Penyelesaian: Gunakan teknik algebra dan sifat fungsi untuk mengasingkan pembolehubah dan mencari penyelesaian.
- Cabaran: Memahami komposisi fungsi. Penyelesaian: Fikirkan komposisi fungsi sebagai fungsi 'berangkai', di mana output satu fungsi menjadi input kepada fungsi yang lain.
- Cabaran: Menerapkan konsep fungsi dalam situasi dunia sebenar. Penyelesaian: Kenal pasti pembolehubah yang terlibat dan cari hubungan matematik yang menggambarkan situasi tersebut.
Soalan Lazim tentang Fungsi Matematik
- Apakah perbezaan antara fungsi dan persamaan? Fungsi adalah peraturan yang menetapkan setiap input kepada satu output unik, manakala persamaan adalah pernyataan matematik yang menunjukkan kesamaan antara dua ungkapan.
- Apakah contoh fungsi linear? Fungsi linear mempunyai graf yang berbentuk garis lurus. Contohnya ialah y = 2x + 1.
- Apakah fungsi kuadratik? Fungsi kuadratik mempunyai graf yang berbentuk parabola. Contohnya ialah y = x^2 - 4x + 3.
- Apakah fungsi trigonometri? Fungsi trigonometri mengaitkan sudut segi tiga dengan nisbah sisi-sisinya. Contohnya ialah sinus, kosinus, dan tangen.
- Apakah aplikasi fungsi dalam kehidupan seharian? Fungsi digunakan dalam pelbagai bidang, seperti fizik, kimia, biologi, ekonomi, dan sains komputer.
- Bagaimana saya boleh meningkatkan pemahaman saya tentang fungsi? Latih tubi, selesaikan masalah, dan jangan takut untuk bertanya!
- Apakah sumber yang berguna untuk mempelajari fungsi? Terdapat banyak buku teks, laman web, dan aplikasi yang didedikasikan untuk mengajar fungsi matematik.
- Apakah kepentingan mempelajari fungsi? Fungsi merupakan asas kepada banyak bidang STEM dan pemahaman yang kukuh tentang fungsi akan membuka banyak peluang kerjaya.
Tips dan Trik Menguasai Fungsi
Selain menguasai asas, visualisasi adalah kunci! Bayangkan fungsi sebagai mesin kecil yang memproses nombor. Gunakan graf, carta, dan apa jua alat yang membantu anda 'melihat' bagaimana fungsi berfungsi. Ingat, amalan membuatkan sempurna. Semakin banyak anda berlatih, semakin mudah untuk anda memahami dan mengaplikasikan konsep fungsi.
Sebagai kesimpulan, fungsi matematik mungkin kelihatan seperti konsep abstrak pada mulanya, tetapi ia sebenarnya adalah alat yang sangat berkuasa untuk memahami dan memodelkan dunia di sekeliling kita. Daripada telefon pintar di tangan anda hingga kepada sistem navigasi GPS dalam kereta anda, fungsi memainkan peranan penting dalam membentuk teknologi moden. Memahami fungsi bukan sahaja membuka pintu kepada dunia matematik yang lebih luas, tetapi juga memupuk pemikiran kritis dan penyelesaian masalah yang penting dalam abad ke-21 ini. Jadi, terokai dunia fungsi matematik yang menakjubkan dan buka kunci potensi penuh anda dalam STEM!

apa itu fungsi pada matematika | Taqueria Autentica
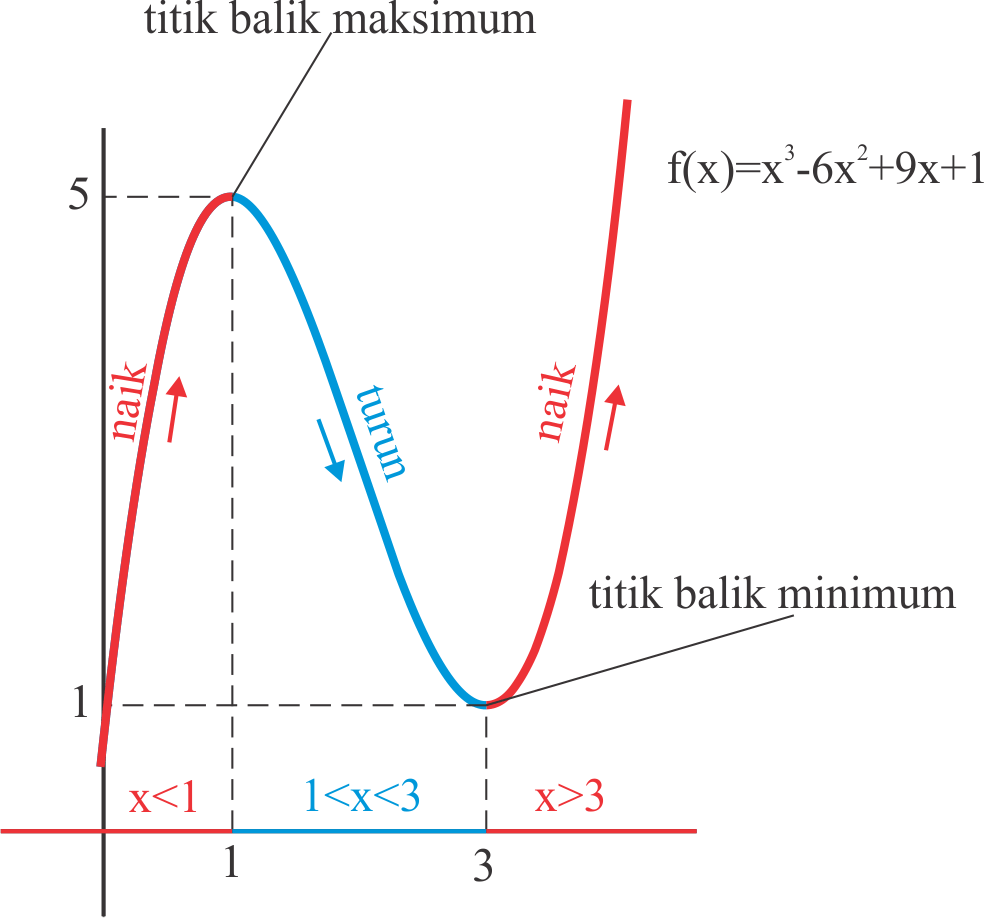
Menentukan Nilai Stasioner dan Jenis Ekstrim Fungsi Pada Matematika | Taqueria Autentica
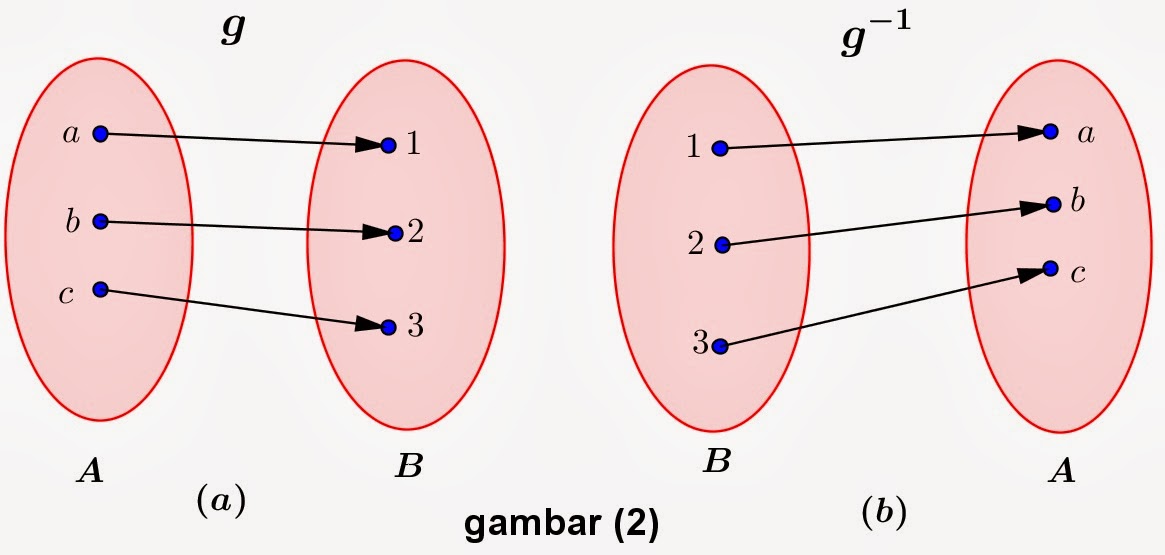
Fungsi Dalam Matematika Adalah | Taqueria Autentica
Simbol Data Pada Flowchart | Taqueria Autentica

apa itu fungsi pada matematika | Taqueria Autentica

apa itu fungsi pada matematika | Taqueria Autentica

apa itu fungsi pada matematika | Taqueria Autentica

Apa Itu Relasi dan Fungsi Dalam Matematika Terlengkap | Taqueria Autentica

Contoh Soal Komposisi Dua Fungsi Atau Lebih | Taqueria Autentica

Memahami Rumus Fungsi Serta Konsepnya Pada Matematika | Taqueria Autentica

apa itu fungsi pada matematika | Taqueria Autentica

Latihan Soal Fungsi Kuadrat Kelas 9 | Taqueria Autentica

Apa Arti Dalam Matematika | Taqueria Autentica

apa itu fungsi pada matematika | Taqueria Autentica
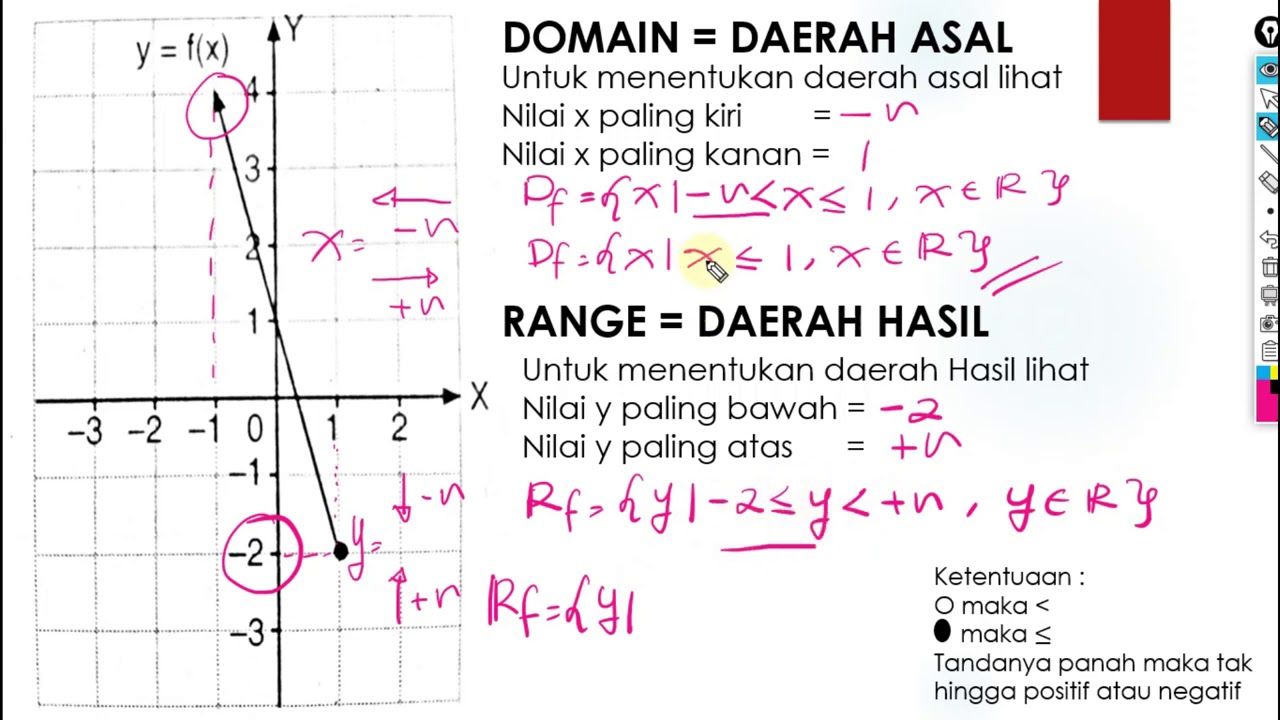
Cara Menentukan Domain Dan Range | Taqueria Autentica