Memahami Arti Set dalam Matematika: Konsep Asas dan Aplikasinya
Pernahkah anda tertanya-tanya bagaimana ahli matematik mengkategorikan dan menganalisis kumpulan objek? Di sinilah konsep 'set' memainkan peranan penting. Dalam dunia matematika, set bukanlah sekadar himpunan objek sembarangan, tetapi entiti yang tertakrif dengan jelas dan mempunyai ciri-ciri unik. Artikel ini akan membawa anda menyelami dunia set, mengupas definisinya, sejarahnya, kepentingannya, serta aplikasinya dalam pelbagai bidang.
Bayangkan anda mempunyai sekumpulan pensel warna. Anda boleh mengkategorikan pensel-pensel ini berdasarkan warna, seperti 'set pensel warna merah', 'set pensel warna biru', dan sebagainya. Setiap kategori ini mewakili satu set. Dalam matematika, set didefinisikan sebagai kumpulan objek atau elemen yang tertakrif dengan jelas. Objek-objek ini boleh berupa apa sahaja, seperti nombor, huruf, bentuk geometri, atau bahkan set lain.
Konsep set diperkenalkan oleh ahli matematik Jerman, Georg Cantor, pada akhir abad ke-19. Cantor merevolusikan cara ahli matematik berfikir tentang infiniti dengan memperkenalkan konsep set tak terhingga dan membangunkan teori set. Teori set menjadi asas kepada hampir semua cabang matematika moden, termasuk algebra, analisis, dan topologi.
Salah satu aspek penting dalam memahami set adalah dengan mengenal pasti elemen-elemennya. Elemen merujuk kepada objek individu yang membentuk set. Contohnya, dalam set nombor genap antara 1 dan 10, elemen-elemennya ialah 2, 4, 6, 8, dan 10. Setiap elemen hanya boleh wujud sekali dalam satu set, dan susunan elemen tidak penting.
Set boleh diwakili dalam dua cara utama: penyenaraian dan tatatanda pembina set. Penyenaraian melibatkan menyenaraikan semua elemen dalam set di antara kurungan kerinting {}. Contohnya, set huruf vokal boleh diwakili sebagai {a, e, i, o, u}. Sebaliknya, tatatanda pembina set mendefinisikan set berdasarkan sifat sepunya yang dikongsi oleh semua elemennya. Contohnya, set nombor ganjil boleh diwakili sebagai {x | x adalah nombor ganjil}.
Kelebihan dan Kekurangan Set dalam Matematika
| Kelebihan | Kekurangan |
|---|---|
| Memudahkan pengelompokan dan analisis data | Boleh menjadi kompleks untuk set dengan bilangan elemen yang sangat besar |
| Membentuk asas kepada banyak cabang matematika lain | Penggunaan tatatanda set yang tidak tepat boleh menyebabkan kekeliruan |
| Membantu dalam menyelesaikan masalah logik dan penaakulan matematik |
Lima Amalan Terbaik Menggunakan Set dalam Matematika
- Gunakan tatatanda set yang betul dan konsisten. Ini membantu mengelakkan kekeliruan dan memastikan kejelasan dalam penyelesaian masalah.
- Fahami perbezaan antara elemen dan set. Elemen adalah objek individu dalam set, manakala set adalah kumpulan objek.
- Kuasai operasi asas set seperti kesatuan, persilangan, dan pelengkap. Operasi ini penting dalam memanipulasi dan menganalisis set.
- Gunakan gambarajah Venn untuk memvisualisasikan hubungan antara set. Gambarajah Venn memudahkan pemahaman konsep set dan operasi set.
- Praktikkan penggunaan set dalam pelbagai konteks matematik. Ini akan mengukuhkan pemahaman anda tentang konsep set dan meningkatkan kemahiran penyelesaian masalah anda.
Lima Contoh Nyata Penggunaan Set dalam Kehidupan
- Pangkalan data: Set digunakan untuk menyimpan dan menyusun data dalam pangkalan data, seperti maklumat pelanggan, produk, dan transaksi.
- Enjin carian: Algoritma enjin carian menggunakan set untuk mencari dan memaparkan hasil carian yang relevan berdasarkan kata kunci yang dimasukkan oleh pengguna.
- Kecerdasan buatan: Set digunakan dalam algoritma pembelajaran mesin untuk mengklasifikasikan dan menganalisis data, seperti pengecaman imej dan pemprosesan bahasa semula jadi.
- Analisis statistik: Set digunakan untuk mewakili populasi dan sampel dalam analisis statistik, membolehkan ahli statistik membuat inferens dan ramalan tentang data.
- Perancangan dan pengurusan projek: Set boleh digunakan untuk memodelkan tugas, sumber, dan kebergantungan dalam projek, memudahkan perancangan dan pengurusan projek yang lebih efisien.
Lima Cabaran dan Penyelesaian Berkaitan Set dalam Matematika
- Cabaran: Memahami konsep set tak terhingga. Penyelesaian: Gunakan analogi dan contoh konkrit untuk menjelaskan konsep infiniti, seperti set nombor asli yang tidak terhingga.
- Cabaran: Membezakan antara subset dan set kuasa. Penyelesaian: Gunakan gambarajah Venn dan contoh untuk menunjukkan perbezaan antara subset, yang merupakan set yang terkandung sepenuhnya dalam set lain, dan set kuasa, yang merupakan set semua subset bagi sesuatu set.
- Cabaran: Menyelesaikan masalah yang melibatkan operasi set kompleks. Penyelesaian: Uraikan masalah kepada langkah-langkah kecil dan gunakan gambarajah Venn untuk menggambarkan setiap langkah.
- Cabaran: Memahami paradoks Russell. Penyelesaian: Kaji sejarah teori set dan paradoks yang timbul daripada definisi set yang naif. Perkenalkan aksiom teori set Zermelo-Fraenkel sebagai penyelesaian kepada paradoks tersebut.
- Cabaran: Menggunakan set dalam konteks aplikasi dunia sebenar. Penyelesaian: Kaitkan konsep set dengan situasi dunia sebenar, seperti pangkalan data, enjin carian, dan analisis statistik.
Soalan Lazim tentang Set dalam Matematika
- Apakah perbezaan antara set dan elemen? Set adalah kumpulan objek, manakala elemen adalah objek individu dalam set.
- Bagaimanakah cara menulis set kosong? Set kosong ditulis sebagai {} atau Ø.
- Apakah set semesta? Set semesta merujuk kepada set yang mengandungi semua elemen yang mungkin dalam konteks tertentu.
- Apakah perbezaan antara kesatuan dan persilangan set? Kesatuan set mengandungi semua elemen dalam kedua-dua set, manakala persilangan set mengandungi hanya elemen yang terdapat dalam kedua-dua set.
- Apakah gambarajah Venn? Gambarajah Venn adalah gambarajah yang digunakan untuk menunjukkan hubungan antara set.
- Apakah aplikasi set dalam kehidupan seharian? Set digunakan dalam pelbagai bidang, termasuk pangkalan data, enjin carian, kecerdasan buatan, dan analisis statistik.
- Apakah kepentingan mempelajari set dalam matematika? Set membentuk asas kepada banyak cabang matematika lain dan penting untuk memahami konsep matematik yang lebih kompleks.
- Apakah sumber yang berguna untuk mempelajari lebih lanjut tentang set? Terdapat banyak buku teks, laman web, dan video dalam talian yang menerangkan konsep set dengan lebih terperinci.
Tips dan Trik Mempelajari Set dalam Matematika
- Mulakan dengan asas: Pastikan anda memahami definisi set, elemen, dan tatatanda set sebelum beralih kepada konsep yang lebih kompleks.
- Visualisasikan set: Gunakan gambarajah Venn untuk membantu anda memvisualisasikan hubungan antara set dan operasi set.
- Latih tubi: Selesaikan banyak latihan dan contoh untuk mengukuhkan pemahaman anda tentang konsep set.
- Cari contoh dalam kehidupan seharian: Cuba kenal pasti bagaimana set digunakan dalam situasi dunia sebenar, seperti dalam pangkalan data, enjin carian, dan analisis statistik.
- Jangan takut untuk bertanya: Jika anda menghadapi kesukaran memahami sesuatu konsep, jangan takut untuk bertanya kepada guru, pensyarah, atau rakan sekelas anda.
Kesimpulannya, set adalah konsep asas dalam matematika yang memainkan peranan penting dalam pelbagai bidang. Memahami definisi, operasi, dan aplikasi set adalah penting untuk membangunkan asas matematik yang kukuh. Dengan menguasai konsep set, anda akan dapat menyelesaikan masalah matematik yang lebih kompleks dan memahami dunia di sekeliling anda dengan lebih baik. Mulakan perjalanan anda untuk meneroka dunia set hari ini dan temui potensi penuh konsep matematik yang menarik ini!

arti set dalam matematika | Taqueria Autentica

Sequence of TAT and the Respective NCL RRM | Taqueria Autentica

Apa Itu Matematika Diskrit | Taqueria Autentica
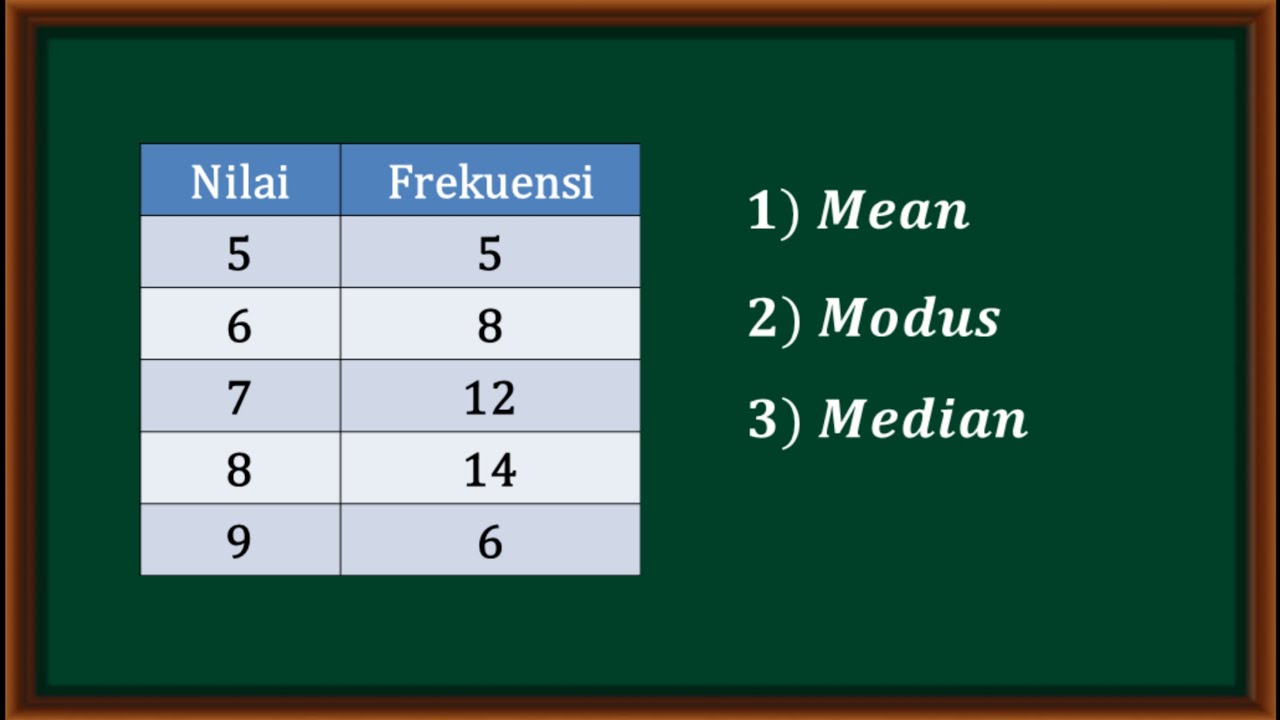
Apa Arti Modus Dalam Matematika | Taqueria Autentica

arti set dalam matematika | Taqueria Autentica

Arti Selisih Dalam Matematika | Taqueria Autentica
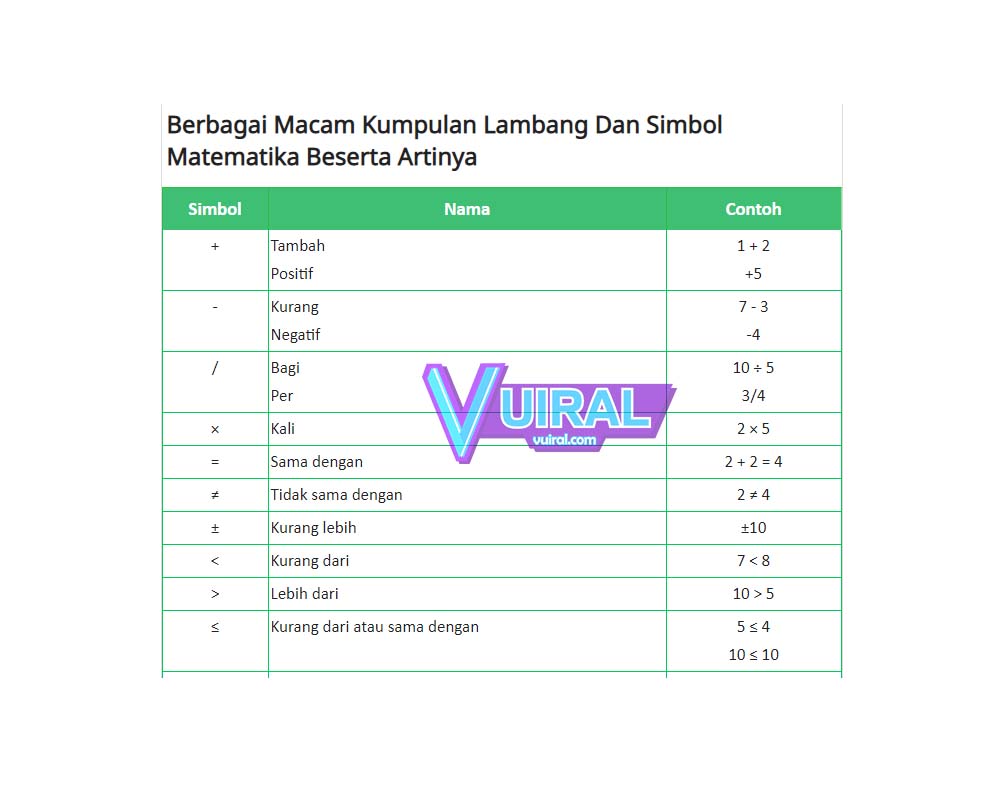
Arti Simbol Dalam Matematika | Taqueria Autentica