Rahsia Rumus Kon: Menguasai Formula Geometri

17 Sep 2024

Rumus Volume Kerucut & Luas Permukaan (+Contoh Soal)

Pernahkah anda memerhatikan bentuk kon ais krim yang sedang mencair di tangan anda? Atau mungkin anda pernah terfikir bagaimana jurutera mengira jumlah konkrit yang diperlukan untuk membina menara berbentuk kon? Di sebalik objek-objek ini tersembunyi rahsia geometri yang menarik – rumus kon.

Rumus kon bukanlah sekadar persamaan matematik yang abstrak. Ia adalah kunci untuk memahami dan menyelesaikan pelbagai masalah praktikal dalam kehidupan seharian. Dengan menguasai rumus ini, kita dapat mengira isipadu kon, luas permukaannya, dan elemen-elemen penting lain seperti panjang garis pelukis dan jejari tapak.

Sejarah rumus kon bermula sejak zaman dahulu lagi. Tamadun purba seperti Mesir dan Mesopotamia telah pun menggunakan konsep kon dalam pembinaan piramid dan ziggurat. Ahli matematik Yunani seperti Archimedes kemudiannya mengembangkan pemahaman tentang geometri kon dan mencipta formula-formula yang masih kita gunakan hari ini.

Salah satu masalah utama yang berkaitan dengan rumus kon ialah kekeliruan dalam mengingati formula yang betul. Terdapat beberapa formula yang berkaitan dengan kon, dan setiap satu mempunyai aplikasi yang berbeza. Sebagai contoh, formula untuk mengira isipadu kon berbeza dengan formula untuk mengira luas permukaannya.

Oleh itu, pemahaman yang mendalam tentang setiap formula dan aplikasinya adalah penting untuk mengelakkan kekeliruan dan memastikan pengiraan yang tepat.

Kelebihan dan Kekurangan Rumus Kon

Kelebihan	Kekurangan
Membantu menyelesaikan masalah praktikal dalam pelbagai bidang.	Boleh menjadi rumit untuk mengingati formula yang betul.
Meningkatkan pemahaman tentang geometri dan konsep ruang.	Memerlukan ketepatan dalam pengiraan untuk mendapatkan hasil yang tepat.
Digunakan secara meluas dalam pelbagai bidang seperti seni bina, kejuruteraan, dan reka bentuk.	Sukar untuk diaplikasikan pada kon yang tidak sempurna atau tidak simetri.

Amalan Terbaik untuk Melaksanakan Rumus Kon

Berikut adalah beberapa amalan terbaik untuk membantu anda menguasai rumus kon:

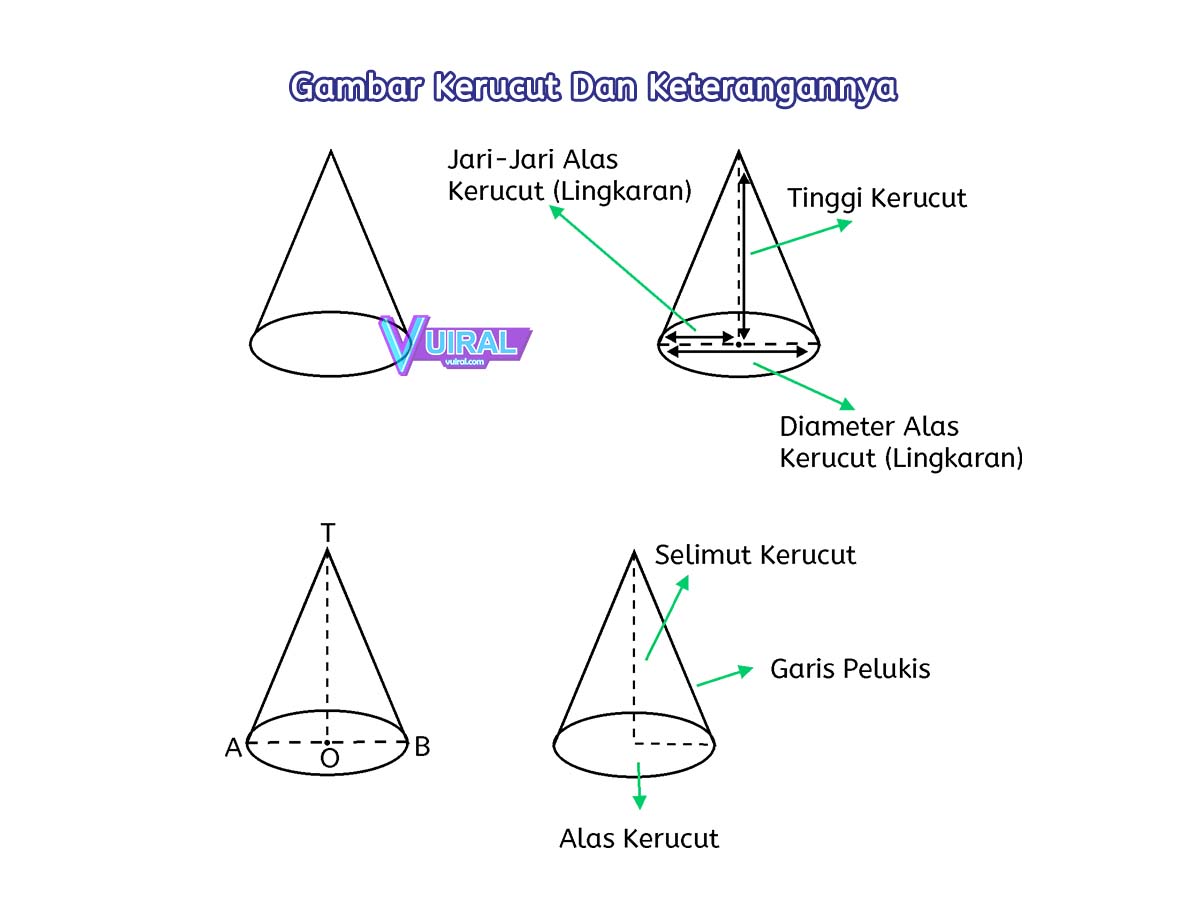
Fahami konsep asas: Sebelum anda mula menghafal formula, pastikan anda memahami konsep asas kon seperti jejari tapak, tinggi, garis pelukis, dan luas permukaan.
Hafal formula yang betul: Terdapat beberapa formula yang berkaitan dengan kon, jadi pastikan anda menghafal formula yang betul untuk setiap pengiraan.
Lakukan latihan yang mencukupi: Latihan yang kerap akan membantu anda mengingati formula dengan lebih baik dan meningkatkan kemahiran pengiraan anda.
Gunakan alat bantu visual: Melukis gambarajah kon dan melabelkan setiap bahagiannya boleh membantu anda memvisualisasikan masalah dengan lebih baik dan memilih formula yang sesuai.
Semak jawapan anda: Selepas menyelesaikan masalah, sentiasa semak semula jawapan anda untuk memastikan ketepatan pengiraan.

Contoh Nyata Rumus Kon

Berikut adalah beberapa contoh nyata bagaimana rumus kon diaplikasikan dalam kehidupan seharian:

Mengira isipadu aiskrim kon.
Merancang dan membina bumbung berbentuk kon.
Menentukan jumlah cecair yang boleh ditampung oleh bekas berbentuk kon.
Mengira jumlah bahan yang diperlukan untuk membuat topi pesta berbentuk kon.
Menganalisis trajektori objek yang bergerak dalam laluan berbentuk kon.

Soalan Lazim

1. Apakah rumus untuk mengira isipadu kon?
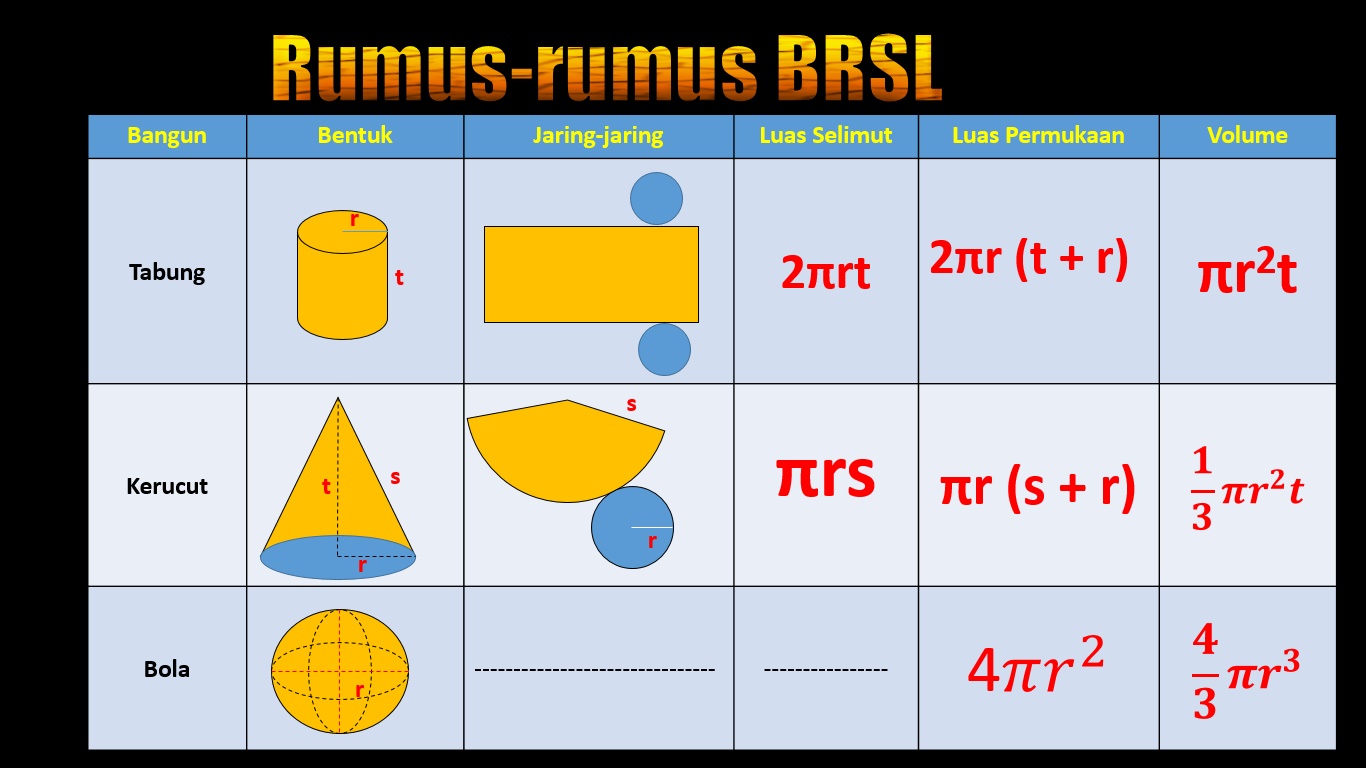
Isipadu kon = (1/3)πr²t, di mana r ialah jejari tapak dan t ialah tinggi kon.

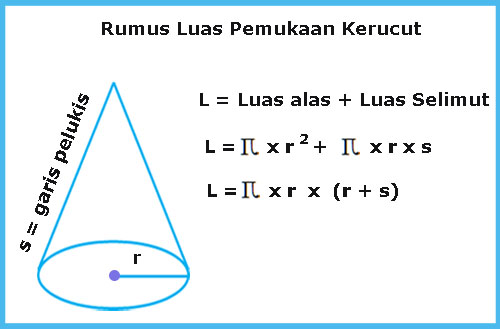
2. Apakah rumus untuk mengira luas permukaan kon?
Luas permukaan kon = πr(r + √(t² + r²)), di mana r ialah jejari tapak dan t ialah tinggi kon.

3. Apakah perbezaan antara tinggi dan garis pelukis kon?
Tinggi kon ialah jarak tegak lurus dari puncak kon ke tapaknya, manakala garis pelukis ialah jarak dari puncak kon ke sebarang titik pada lilitan tapaknya.

4. Apakah aplikasi rumus kon dalam kehidupan seharian?
Rumus kon digunakan dalam pelbagai bidang seperti seni bina, kejuruteraan, reka bentuk, dan sains untuk mengira isipadu, luas permukaan, dan elemen-elemen lain bagi objek berbentuk kon.

5. Bagaimana saya boleh mengingati rumus kon dengan mudah?
Anda boleh mengingati rumus kon dengan lebih mudah melalui latihan yang kerap, menggunakan alat bantu visual, dan mengaitkan formula dengan aplikasi praktikal.

6. Apakah beberapa sumber yang berguna untuk mempelajari lebih lanjut tentang rumus kon?
Terdapat banyak sumber yang berguna untuk mempelajari lebih lanjut tentang rumus kon, termasuk buku teks matematik, laman web pendidikan, dan video tutorial dalam talian.

7. Adakah terdapat aplikasi atau perisian yang boleh membantu saya menyelesaikan masalah yang berkaitan dengan rumus kon?
Ya, terdapat beberapa aplikasi dan perisian yang boleh membantu anda menyelesaikan masalah yang berkaitan dengan rumus kon, seperti kalkulator geometri dan perisian pemodelan 3D.

8. Apakah beberapa cabaran yang mungkin saya hadapi ketika menggunakan rumus kon, dan bagaimana saya boleh mengatasinya?
Salah satu cabaran yang mungkin anda hadapi ialah kekeliruan dalam memilih formula yang betul. Untuk mengatasi cabaran ini, pastikan anda memahami konsep asas kon dan aplikasi setiap formula. Anda juga boleh menggunakan alat bantu visual seperti gambarajah untuk membantu anda memvisualisasikan masalah dan memilih formula yang sesuai.

Tips dan Trik

Untuk memudahkan pengiraan rumus kon, anda boleh menggunakan kalkulator saintifik atau aplikasi kalkulator geometri pada telefon pintar. Pastikan anda memasukkan nilai yang tepat untuk jejari, tinggi, dan garis pelukis untuk mendapatkan hasil yang tepat.

Kesimpulan

Rumus kon merupakan alat yang penting dalam matematik dan mempunyai pelbagai aplikasi dalam kehidupan seharian. Memahami dan menguasai rumus ini bukan sahaja membantu dalam menyelesaikan masalah geometri, tetapi juga meningkatkan keupayaan kita untuk berfikir secara kritikal dan menyelesaikan masalah dalam pelbagai konteks. Dengan latihan yang konsisten dan pendekatan yang betul, sesiapa sahaja boleh menguasai rahsia rumus kon dan memanfaatkan potensinya sepenuhnya.