Rahsia Tersembunyi Disebalik Bilangan Bulat: Lebih Daripada Yang Anda Tahu!

18 Jun 2024

Pernahkah anda terfikir tentang kepentingan nombor dalam kehidupan seharian kita? Daripada mengira wang saku hinggalah mengukur bahan masakan, nombor memainkan peranan penting. Tetapi tahukah anda bahawa satu jenis nombor, yang dikenali sebagai "bilangan bulat," menyimpan rahsia dan keajaiban matematik yang menakjubkan?

Dalam pengembaraan matematik ini, kita akan menyelami dunia bilangan bulat, menyingkap rahsia mereka yang tersembunyi, dan meneroka bagaimana mereka membentuk dunia di sekeliling kita. Bersiaplah untuk kagum dengan kepentingan, aplikasi praktikal, dan potensi tersembunyi bilangan bulat!

Bayangkan sebuah dunia tanpa nombor. Bagaimana kita boleh mengira masa, mengukur jarak, atau menjalankan transaksi kewangan? Bilangan bulat membentuk asas aritmetik, membolehkan kita melakukan operasi asas seperti tambah, tolak, darab, dan bahagi. Tanpa mereka, matematik akan menjadi sesuatu yang mustahil, melumpuhkan kemajuan saintifik dan teknologi.

Asal-usul bilangan bulat dapat dikesan kembali ke zaman purba. Tamadun awal seperti Babylon dan Mesir menggunakan sistem nombor berdasarkan bilangan bulat untuk tujuan praktikal seperti perdagangan, astronomi, dan pembinaan. Seiring dengan berlalunya masa, konsep bilangan bulat berkembang, membawa kepada perkembangan sistem nombor yang lebih kompleks yang kita gunakan hari ini.

Tetapi bilangan bulat bukan sekadar alat matematik abstrak. Mereka mempunyai implikasi yang mendalam dalam pelbagai bidang, termasuk sains komputer, fizik, dan kejuruteraan. Dalam sains komputer, bilangan bulat digunakan untuk mewakili data digital, membolehkan komputer memproses maklumat dengan cekap. Dalam fizik, mereka digunakan untuk menerangkan kuantiti fizik seperti cas elektrik dan momentum sudut. Dalam kejuruteraan, mereka adalah penting untuk reka bentuk struktur, litar elektronik, dan sistem lain yang banyak.

Kelebihan dan Kekurangan Bilangan Bulat

Walaupun mempunyai banyak kelebihan, bilangan bulat juga mempunyai beberapa batasan yang perlu dipertimbangkan:

Kelebihan	Kekurangan
Mudah difahami dan digunakan	Tidak dapat mewakili kuantiti pecahan
Sesuai untuk mewakili kuantiti diskret	Boleh menyebabkan ralat pembundaran dalam beberapa pengiraan
Diproses dengan cekap oleh komputer	Julat terhad berbanding dengan nombor lain seperti nombor nyata

Lima Amalan Terbaik untuk Menggunakan Bilangan Bulat

Berikut adalah lima amalan terbaik untuk menggunakan bilangan bulat dengan berkesan:

Pilih jenis data yang betul: Bahasa pengaturcaraan menawarkan pelbagai jenis data integer, setiap satu dengan julat dan ketepatannya sendiri. Memilih jenis data yang betul boleh membantu mengelakkan ralat limpahan dan meningkatkan kecekapan kod.
Gunakan pemalar apabila sesuai: Pemalar ialah nilai yang tidak berubah sepanjang pelaksanaan program. Menggunakan pemalar untuk mewakili nilai integer yang diketahui boleh meningkatkan kebolehbacaan dan kebolehubahan kod.
Gunakan operasi bitwise dengan berhati-hati: Operasi bitwise boleh menjadi sangat cekap tetapi juga sukar difahami dan diselenggara. Gunakannya dengan berhati-hati dan pastikan kod anda didokumenkan dengan baik.
Uji kod anda dengan teliti: Seperti mana-mana bahagian kod, adalah penting untuk menguji kod anda dengan teliti untuk memastikan ia berfungsi seperti yang diharapkan. Gunakan pelbagai input dan kes ujian untuk mengesahkan ketepatan kod anda.
Rujukan dokumentasi: Jika anda tidak pasti tentang aspek tertentu penggunaan integer, rujuk dokumentasi bahasa pengaturcaraan atau platform yang anda gunakan. Dokumentasi boleh memberikan maklumat dan contoh yang berharga.

Contoh Nyata Bilangan Bulat dalam Tindakan

Berikut adalah lima contoh nyata bagaimana bilangan bulat digunakan dalam kehidupan seharian:

Urus niaga kewangan: Bilangan bulat digunakan untuk mewakili jumlah wang dalam urus niaga kewangan, memastikan ketepatan dan mencegah penipuan.
Pengaturcaraan komputer: Bilangan bulat adalah asas kepada bahasa pengaturcaraan, digunakan untuk mewakili data, mengawal aliran program, dan mengurus memori.
Kriptografi: Bilangan bulat memainkan peranan penting dalam algoritma penyulitan, memastikan keselamatan data sensitif dan komunikasi dalam talian.
Analisis data: Bilangan bulat digunakan dalam set data yang besar untuk mewakili pembolehubah diskret, seperti umur, bilangan anak, atau penarafan produk.
Navigasi GPS: Sistem GPS menggunakan bilangan bulat untuk mewakili lokasi, masa, dan data lain yang diperlukan untuk pengiraan kedudukan yang tepat.

Cabaran dan Penyelesaian

Walaupun bilangan bulat adalah penting dalam pelbagai bidang, penggunaannya juga boleh menimbulkan cabaran tertentu. Mari kita terokai beberapa cabaran ini dan penyelesaian yang berpotensi:

Limpahan Integer: Limpahan integer berlaku apabila nilai integer melebihi julat yang boleh diwakili oleh jenis data tertentu. Ini boleh menyebabkan hasil yang tidak dijangka dan ralat dalam program. Penyelesaian: Gunakan jenis data integer yang lebih besar, melaksanakan pengendalian ralat, atau menggunakan teknik pengaturcaraan untuk mengelakkan limpahan.
Ralat Pembundaran: Apabila melakukan operasi aritmetik pada bilangan bulat, ralat pembundaran boleh berlaku, yang membawa kepada kehilangan ketepatan. Penyelesaian: Gunakan jenis data titik terapung untuk pengiraan yang memerlukan ketepatan yang lebih tinggi, atau laksanakan teknik pembundaran untuk meminimumkan ralat.
Kecekapan: Dalam beberapa kes, operasi integer mungkin tidak secekap operasi yang melibatkan jenis data lain, seperti nombor titik terapung. Penyelesaian: Gunakan algoritma dan struktur data yang dioptimumkan, manfaatkan perkakasan khusus seperti unit titik terapung, atau pertimbangkan untuk menggunakan jenis data alternatif apabila sesuai.
Keselamatan: Limpahan integer dan kelemahan berkaitan integer lain boleh dieksploitasi oleh penyerang untuk menyebabkan penafian perkhidmatan atau melaksanakan kod berniat jahat. Penyelesaian: Gunakan amalan pengekodan selamat, sahkan input pengguna dengan teliti, dan pastikan perisian dikemas kini dengan tampalan keselamatan terkini.
Kebolehbacaan Kod: Operasi bitwise dan manipulasi integer peringkat rendah boleh menjejaskan kebolehbacaan kod, menjadikannya mencabar untuk difahami dan diselenggara oleh pembangun lain. Penyelesaian: Gunakan komen yang jelas dan ringkas, ikuti konvensyen penamaan yang konsisten, dan pertimbangkan untuk membagi kod kompleks kepada fungsi atau modul yang lebih kecil.

Soalan Lazim

Berikut adalah beberapa soalan lazim tentang bilangan bulat:

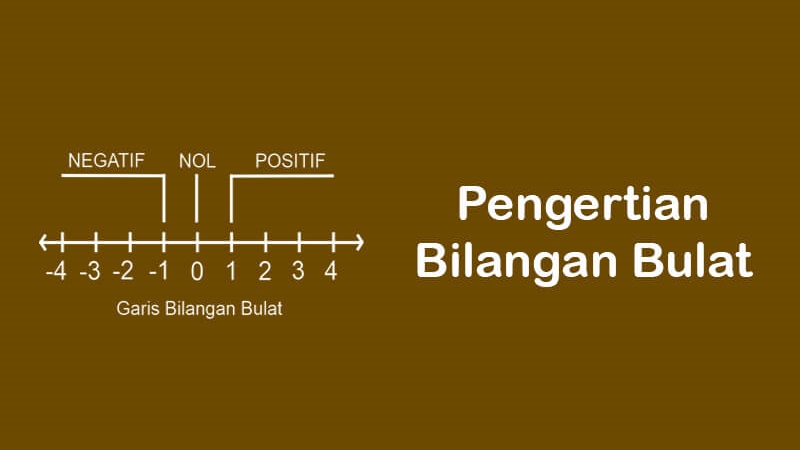
Apakah bilangan bulat? Bilangan bulat ialah nombor bulat (bukan pecahan) yang boleh positif, negatif, atau sifar.
Apakah perbezaan antara bilangan bulat dan nombor nyata? Nombor nyata termasuk nombor pecahan dan perpuluhan, manakala bilangan bulat hanya nombor bulat.
Apakah beberapa jenis data integer biasa dalam bahasa pengaturcaraan? Int, short, long, dan byte ialah beberapa jenis data integer biasa.
Bagaimanakah bilangan bulat digunakan dalam sains komputer? Bilangan bulat digunakan untuk mewakili data, mengawal aliran program, dan mengurus memori dalam sains komputer.
Apakah limpahan integer? Limpahan integer berlaku apabila nilai integer cuba melebihi had storan jenis datanya.
Apakah aplikasi bilangan bulat dalam kehidupan seharian? Bilangan bulat digunakan dalam pelbagai aplikasi, seperti kewangan, pengaturcaraan komputer, dan analisis data.
Apakah beberapa cabaran dalam menggunakan bilangan bulat? Cabaran termasuk limpahan integer, ralat pembundaran, dan kebimbangan keselamatan yang berpotensi.
Apakah beberapa sumber untuk mempelajari lebih lanjut tentang bilangan bulat? Buku teks matematik, tutorial dalam talian, dan dokumentasi bahasa pengaturcaraan ialah sumber yang hebat untuk mempelajari lebih lanjut tentang bilangan bulat.

Tips dan Trik untuk Bekerja dengan Bilangan Bulat

Berikut adalah beberapa petua dan trik tambahan untuk bekerja dengan bilangan bulat dengan berkesan:

Biasakan diri anda dengan operator integer yang berbeza dan keutamaannya.
Gunakan operasi modulo (%) untuk mengira baki pembahagian integer.
Fahami perbezaan antara pembahagian integer dan pembahagian titik terapung.
Gunakan fungsi matematik terbina dalam untuk operasi integer biasa, seperti nilai mutlak, pembundaran, dan pemotongan.
Pertimbangkan untuk menggunakan perpustakaan matematik atau modul untuk operasi integer yang lebih maju.

Sebagai kesimpulan, bilangan bulat ialah konsep asas dalam matematik dan sains komputer yang memainkan peranan penting dalam kehidupan seharian kita. Daripada mengira objek hingga mewakili data digital, bilangan bulat membentuk asas aritmetik dan banyak aplikasi praktikal. Memahami sifat, operasi, dan potensi cabaran yang berkaitan dengan bilangan bulat adalah penting untuk pelbagai usaha, termasuk pengaturcaraan, analisis data, dan penyelesaian masalah dalam pelbagai bidang. Sama ada anda seorang pelajar, profesional, atau hanya ingin tahu tentang dunia di sekeliling anda, meluangkan masa untuk menghargai kepentingan bilangan bulat boleh membuka kunci pemahaman yang lebih mendalam tentang subjek yang menarik ini dan aplikasi meluasnya.