Rahsia Tersembunyi: Menyingkap Keajaiban Rumus Bangun Ruang
Pernahkah anda merenung keajaiban piramid Mesir atau keanggunan Menara Condong Pisa? Struktur-struktur ikonik ini, bersama-sama dengan objek-objek biasa seperti kotak kasut dan bola sepak, berkongsi satu persamaan asas: kesemuanya merupakan contoh bangun ruang. Memahami rumus yang mengawal bentuk-bentuk tiga dimensi ini membuka pintu kepada dunia ilmu pengetahuan, seni bina, dan reka bentuk yang menakjubkan.
Sejak zaman dahulu kala, manusia telah berusaha untuk mengukur dan memahami ruang di sekeliling mereka. Orang Mesir purba, misalnya, menggunakan geometri praktikal untuk membina piramid mereka dengan ketepatan yang menakjubkan. Sumbangan cendekiawan Yunani seperti Euclid dan Pythagoras meletakkan asas kukuh bagi geometri ruang, yang kemudiannya dikembangkan oleh tamadun-tamadun lain.
Rumus bangun ruang bukan sekadar persamaan abstrak yang terkurung dalam buku teks. Sebaliknya, ia adalah alat yang berkuasa yang membolehkan kita mengira isipadu kotak untuk penghantaran, mereka bentuk jambatan yang kukuh, dan juga memahami pergerakan planet di angkasa lepas.
Salah satu manfaat utama menguasai rumus bangun ruang ialah keupayaan untuk mengira isipadu dan luas permukaan sesuatu objek. Sebagai contoh, dengan mengetahui rumus isipadu kubus (sisi x sisi x sisi), kita boleh dengan mudah menentukan jumlah ruang yang boleh diisi oleh kotak berbentuk kubus. Begitu juga, rumus luas permukaan sfera (4πjejari²) membolehkan kita mengira jumlah bahan yang diperlukan untuk menutupi permukaan bola sepenuhnya.
Selain itu, pemahaman yang kukuh tentang rumus bangun ruang adalah penting dalam pelbagai bidang kerjaya, seperti seni bina, kejuruteraan, dan reka bentuk. Arkitek menggunakan rumus ini untuk mereka bentuk bangunan yang selamat dan estetik, manakala jurutera bergantung padanya untuk mengira beban dan daya pada struktur. Pereka bentuk grafik dan animator menggunakan rumus geometri ruang untuk mencipta imej dan animasi tiga dimensi yang realistik.
Walaupun manfaatnya banyak, memahami dan mengingati rumus bangun ruang boleh menjadi satu cabaran bagi sesetengah pelajar. Walau bagaimanapun, dengan pendekatan pembelajaran yang betul dan latihan yang konsisten, sesiapa sahaja boleh menguasai konsep-konsep ini.
Kelebihan dan Kekurangan Mempelajari Rumus Bangun Ruang
| Kelebihan | Kekurangan |
|---|---|
| Meningkatkan kemahiran menyelesaikan masalah spatial. | Boleh menjadi sukar untuk memvisualisasikan bentuk 3D. |
| Aplikasi praktikal dalam kehidupan seharian dan pelbagai bidang kerjaya. | Memerlukan pemahaman yang kukuh tentang konsep geometri asas. |
| Membuka pintu kepada bidang pengajian STEM yang lebih tinggi. | Menghafal pelbagai rumus boleh menjadi satu cabaran. |
Lima Amalan Terbaik untuk Mempelajari Rumus Bangun Ruang
- Visualisasikan bentuk: Gunakan objek konkrit, model 3D, atau perisian visualisasi untuk membantu anda memahami bentuk dan sifat-sifatnya.
- Latih tubi dengan contoh: Selesaikan pelbagai masalah latihan untuk mengukuhkan pemahaman anda tentang rumus dan aplikasi mereka.
- Pecahkan masalah kepada langkah-langkah kecil: Jangan cuba menghafal rumus secara membuta tuli. Sebaliknya, fahami setiap pemboleh ubah dan bagaimana ia berkaitan dengan bentuk tersebut.
- Cari corak dan hubungan: Banyak rumus bangun ruang saling berkaitan. Mengenal pasti corak ini boleh memudahkan proses pembelajaran.
- Jangan takut untuk meminta bantuan: Jika anda menghadapi kesukaran, jangan teragak-agak untuk meminta bantuan guru, tutor, atau rakan sekelas.
Lima Contoh Nyata Aplikasi Rumus Bangun Ruang
- Seni bina: Arkitek menggunakan rumus bangun ruang untuk mengira jumlah bahan yang diperlukan untuk membina bangunan, menentukan kestabilan struktur, dan mereka bentuk ruang dalaman yang berfungsi.
- Kejuruteraan: Jurutera menggunakan rumus ini untuk mereka bentuk jambatan, terowong, dan struktur lain yang kukuh dan selamat. Mereka juga menggunakannya untuk mengira aliran cecair melalui paip dan daya aerodinamik pada pesawat.
- Reka bentuk: Pereka grafik, pereka produk, dan animator menggunakan rumus bangun ruang untuk mencipta model 3D, visualisasi data, dan animasi yang realistik.
- Sains: Ahli kimia menggunakan rumus ini untuk memahami struktur molekul, manakala ahli astronomi menggunakannya untuk mengira jarak dan saiz objek angkasa.
- Kehidupan seharian: Kita menggunakan rumus bangun ruang untuk mengira isipadu bekas, menganggar jumlah cat yang diperlukan untuk mengecat bilik, dan membungkus hadiah.
Lima Cabaran dan Penyelesaian Berkaitan dengan Rumus Bangun Ruang
- Cabaran: Kesukaran memvisualisasikan bentuk 3D.
Penyelesaian: Gunakan model fizikal, perisian visualisasi, dan lukis gambarajah untuk membantu membayangkan bentuk. - Cabaran: Menghafal banyak rumus.
Penyelesaian: Fokus pada pemahaman konsep dan terbitkan rumus daripada pemahaman tersebut. Gunakan kad imbasan atau teknik mnemonik untuk membantu menghafal. - Cabaran: Mengenal pasti rumus yang betul untuk digunakan dalam situasi tertentu.
Penyelesaian: Latih tubi menyelesaikan pelbagai masalah dan belajar menganalisis masalah untuk mengenal pasti maklumat yang diberikan dan apa yang perlu dicari. - Cabaran: Menyelesaikan masalah yang melibatkan bentuk kompleks.
Penyelesaian: Pecahkan bentuk kompleks kepada bentuk yang lebih mudah dan gunakan rumus yang sesuai untuk setiap bahagian. Lukis gambarajah untuk membantu memvisualisasikan proses ini. - Cabaran: Kekurangan keyakinan dalam menggunakan rumus bangun ruang.
Penyelesaian: Mulakan dengan masalah yang lebih mudah dan tingkatkan tahap kesukaran secara beransur-ansur. Raikan kejayaan anda dan ingat bahawa latihan menjadikan sempurna.
Soalan Lazim tentang Rumus Bangun Ruang
- Apakah perbezaan antara isipadu dan luas permukaan?
Isipadu merujuk kepada jumlah ruang yang diisi oleh objek 3D, manakala luas permukaan merujuk kepada jumlah luas semua permukaan luar objek. - Apakah rumus untuk mengira isipadu kubus?
Isipadu kubus = sisi x sisi x sisi - Apakah rumus untuk mengira luas permukaan sfera?
Luas permukaan sfera = 4πjejari² - Apakah aplikasi praktikal rumus bangun ruang dalam kehidupan seharian?
Kita menggunakan rumus ini untuk mengira isipadu bekas, menganggar jumlah cat yang diperlukan, membungkus hadiah, dan banyak lagi. - Apakah beberapa kerjaya yang memerlukan pemahaman yang kukuh tentang rumus bangun ruang?
Kerjaya seperti arkitek, jurutera, pereka grafik, dan saintis memerlukan pemahaman yang kukuh tentang rumus bangun ruang. - Apakah beberapa sumber yang berguna untuk mempelajari lebih lanjut tentang rumus bangun ruang?
Buku teks matematik, laman web pendidikan, video dalam talian, dan tutor boleh memberi sokongan tambahan. - Apakah terdapat helah untuk mengingati rumus bangun ruang dengan lebih mudah?
Ya, gunakan kad imbasan, teknik mnemonik, atau kaitkan rumus dengan lagu atau rima untuk memudahkan penghafalan. - Mengapa penting untuk mempelajari rumus bangun ruang?
Mempelajari rumus bangun ruang meningkatkan kemahiran menyelesaikan masalah, menyediakan asas untuk bidang STEM yang lebih tinggi, dan mempunyai aplikasi praktikal dalam kehidupan seharian dan pelbagai kerjaya.
Tips dan Trik Mempelajari Rumus Bangun Ruang
- Gunakan warna yang berbeza untuk menandakan bahagian rumus yang berbeza.
- Buat carta atau jadual untuk meringkaskan rumus penting.
- Ajar orang lain tentang rumus yang telah anda pelajari untuk mengukuhkan pemahaman anda sendiri.
- Cari aplikasi dunia nyata rumus untuk menjadikan pembelajaran lebih relevan.
- Berlatih, berlatih, berlatih! Semakin banyak anda berlatih, semakin yakin anda akan menjadi.
Kesimpulannya, menguasai rumus bangun ruang merupakan satu perjalanan yang bermanfaat yang membuka pintu kepada pemahaman yang lebih mendalam tentang dunia di sekeliling kita. Walaupun ia mungkin kelihatan mencabar pada mulanya, dengan kesabaran, latihan yang konsisten, dan pendekatan pembelajaran yang betul, sesiapa sahaja boleh menguasai konsep-konsep ini. Ingatlah untuk memecahkan masalah kepada langkah-langkah kecil, memvisualisasikan bentuk, dan jangan takut untuk meminta bantuan apabila diperlukan. Teruskan meneroka dunia geometri ruang yang menakjubkan dan temukan keajaiban tersembunyi yang menanti anda!

Volume dan Luas Permukaan Kerucut | Taqueria Autentica

Sifat Sifat Bangun Ruang Limas Segitiga Dan Rumusnya Serta Contoh | Taqueria Autentica

Rumus Bangun Ruang Dan Contoh Soal Studyhelp | Taqueria Autentica

semua rumus bangun ruang | Taqueria Autentica

Student Life Hacks, Life Hacks For School, Math Infographic, Study | Taqueria Autentica

Rumus Bangun Ruang Dan Gambarnya | Taqueria Autentica
.jpg)
Rumus Bangun Ruang: Kubus, Balok, Tabung, Bola dll Beserta Gambar | Taqueria Autentica

Detail Rumus Bangun Ruang Dan Contoh Soal Koleksi Nomer 55 | Taqueria Autentica
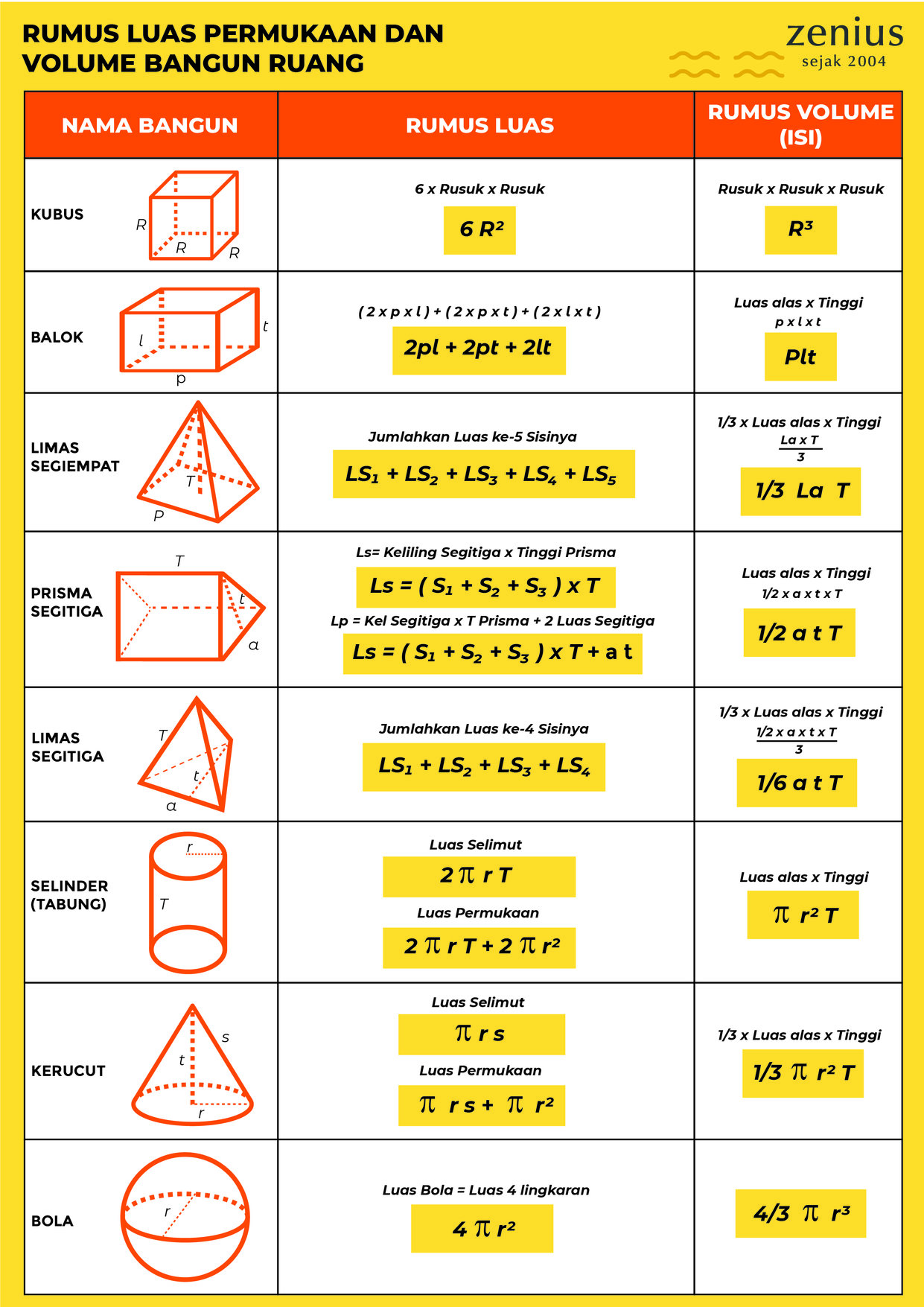
Rumus Bangun Ruang Menghitung Volume Luas Permukaan Dan Contoh Soal | Taqueria Autentica

Daftar Lengkap Rumus Bangun Ruang (Kubus, Balok, Tabung, Bola, Dll | Taqueria Autentica
Gambar Menarik Bangun rumus | Taqueria Autentica

Volume Bangun Ruang Tabung Adalah 3 Kali Dari Volume Bangun Ruang | Taqueria Autentica

Daftar Lengkap Rumus Bangun Ruang (Kubus, Balok, Tabung, Bola, Dll) Kunjaw | Taqueria Autentica

Rumus Bangun Datar dan Bangun Ruang | Taqueria Autentica