Tanda Seru dalam Matematik: Lebih Daripada Sekadar Ungkapan Terkejut!
Pernahkah anda terjumpa tanda seru (!) dalam persamaan matematik dan tertanya-tanya apa maksudnya? Jangan risau, anda tidak keseorangan! Tanda seru dalam matematik bukanlah sekadar tanda untuk menunjukkan keterujaan atau kejutan, tetapi ia mempunyai makna yang lebih mendalam dan penting dalam dunia nombor.
Dalam matematik, tanda seru dikenali sebagai "faktorial". Ia mungkin kelihatan seperti simbol yang mudah, tetapi ia mewakili operasi matematik yang sangat berguna, terutamanya dalam bidang kebarangkalian, kombinatorik, dan kalkulus. Memahami konsep faktorial adalah penting untuk menyelesaikan pelbagai masalah matematik dan menghargai keindahan dan keanggunan bahasa nombor.
Secara ringkasnya, faktorial sesuatu nombor bulat positif ialah hasil darab semua nombor bulat positif yang kurang daripada atau sama dengan nombor itu. Contohnya, faktorial 5, ditulis sebagai 5!, ialah 5 x 4 x 3 x 2 x 1, yang sama dengan 120. Faktorial 0, dilambangkan sebagai 0!, ditakrifkan sebagai 1. Definisi ini mungkin kelihatan aneh pada mulanya, tetapi ia memainkan peranan penting dalam pelbagai teorem dan formula matematik.
Faktorial mempunyai sejarah yang panjang dan menarik, yang boleh dikesan kembali ke zaman ahli matematik Babylon purba. Walau bagaimanapun, notasi moden yang menggunakan tanda seru (!) diperkenalkan pada awal abad ke-19 oleh ahli matematik Perancis, Christian Kramp. Sejak itu, faktorial telah menjadi konsep asas dalam matematik, dengan aplikasi dalam pelbagai bidang, termasuk statistik, fizik, dan sains komputer.
Salah satu aplikasi utama faktorial ialah dalam mengira bilangan cara untuk menyusun atau menggabungkan objek. Contohnya, katakan anda mempunyai 5 buah buku yang berbeza dan anda ingin menyusunnya di rak buku. Berapa banyak susunan yang mungkin? Jawapannya ialah 5!, atau 120. Ini kerana anda mempunyai 5 pilihan untuk buku pertama, kemudian 4 pilihan untuk buku kedua, dan seterusnya. Secara amnya, bilangan cara untuk menyusun n objek ialah n!.
Kelebihan dan Kekurangan Faktorial
Seperti mana-mana konsep matematik, faktorial mempunyai kelebihan dan kekurangan tersendiri. Memahami perkara ini boleh membantu anda menghargai lebih mendalam tentang kegunaan dan batasannya.
| Kelebihan | Kekurangan |
|---|---|
| Menyederhanakan pengiraan dalam kebarangkalian dan kombinatorik | Boleh menghasilkan nombor yang sangat besar dengan cepat, menjadikannya sukar untuk dikendalikan |
| Mempunyai aplikasi dalam pelbagai bidang matematik | Tidak ditakrifkan untuk nombor negatif atau bukan integer |
Amalan Terbaik untuk Menggunakan Faktorial
Berikut adalah beberapa amalan terbaik untuk menggunakan faktorial dengan berkesan dan tepat:
- Fahami definisi: Pastikan anda memahami sepenuhnya definisi faktorial sebelum menggunakannya dalam pengiraan.
- Gunakan kalkulator atau perisian: Untuk nombor besar, mengira faktorial secara manual boleh menjadi memakan masa dan terdedah kepada ralat. Gunakan kalkulator atau perisian yang mempunyai fungsi faktorial.
- Permudahkan ungkapan: Apabila mungkin, permudahkan ungkapan faktorial sebelum mengiranya. Contohnya, n!/ (n-1)! boleh dipermudahkan kepada n.
- Berhati-hati dengan nombor besar: Faktorial boleh menghasilkan nombor yang sangat besar dengan cepat. Berhati-hati dengan potensi limpahan atau ralat dalam pengiraan anda.
- Gunakan dalam konteks yang sesuai: Faktorial paling berguna dalam masalah yang melibatkan susunan, kombinasi, dan kebarangkalian. Gunakannya dengan bijak dalam konteks ini.
Soalan Lazim tentang Faktorial
Berikut adalah beberapa soalan lazim tentang faktorial:
- Apakah faktorial 0? Faktorial 0 ditakrifkan sebagai 1.
- Bolehkah faktorial nombor negatif dikira? Tidak, faktorial hanya ditakrifkan untuk nombor bulat positif.
- Apakah aplikasi faktorial dalam kehidupan sebenar? Faktorial digunakan dalam pelbagai bidang, seperti kebarangkalian (contohnya, mengira bilangan tangan yang mungkin dalam permainan kad), statistik, dan fizik.
- Apakah perbezaan antara permutasi dan kombinasi? Permutasi ialah susunan objek yang tersusun, manakala kombinasi ialah pemilihan objek yang tidak tersusun.
Kesimpulannya, tanda seru, atau faktorial, ialah konsep penting dalam matematik yang mempunyai pelbagai aplikasi dalam pelbagai bidang. Memahami definisi, sifat, dan aplikasi faktorial boleh meningkatkan kemahiran matematik anda dan membuka pintu kepada konsep matematik yang lebih maju. Jadi, lain kali anda melihat tanda seru dalam persamaan matematik, ingatlah bahawa ia lebih daripada sekadar ungkapan terkejut - ia adalah simbol operasi matematik yang kuat dengan sejarah dan kegunaan yang kaya!
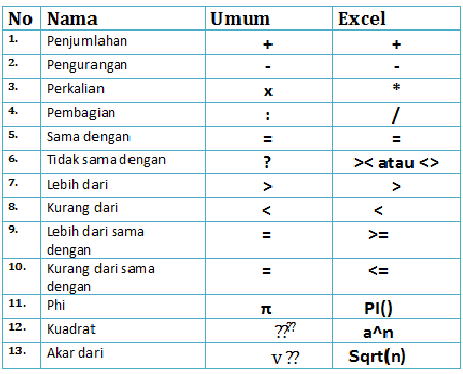
apa arti tanda seru dalam matematika | Taqueria Autentica

Ivan Lanin @ivanlanin , Twitter Profile | Taqueria Autentica

Tanda Sama Dengan Dalam Matematika | Taqueria Autentica

apa arti tanda seru dalam matematika | Taqueria Autentica

Arti Simbol Bahan Kimia Berbahaya | Taqueria Autentica
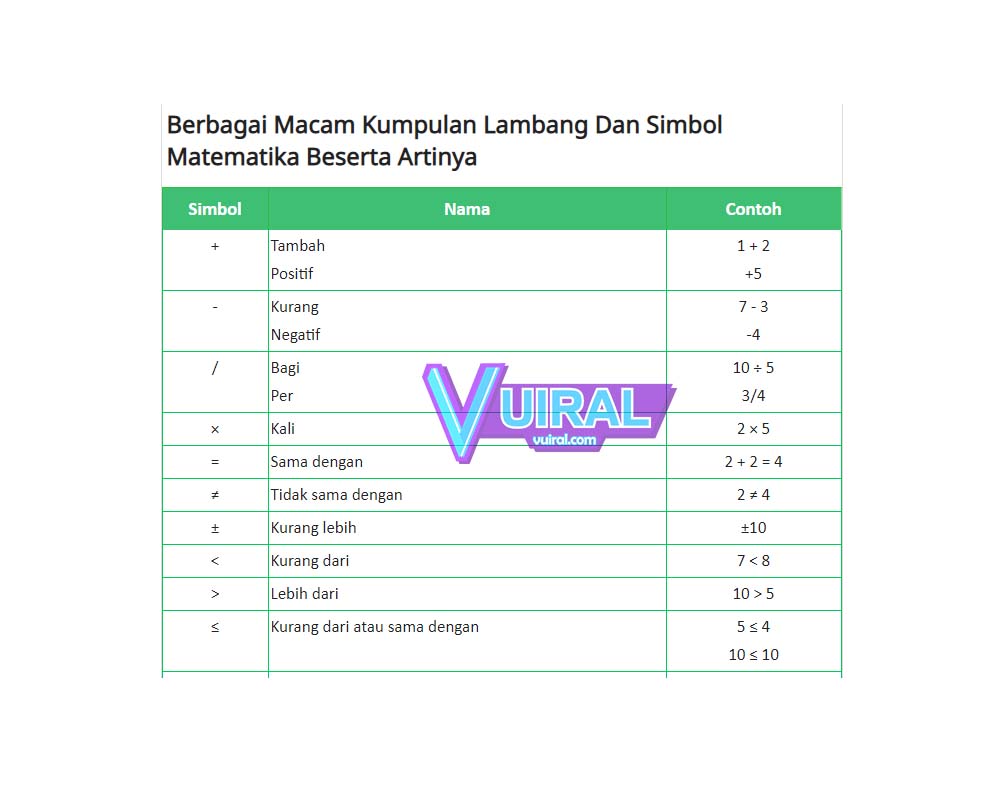
Arti Simbol Dalam Matematika | Taqueria Autentica
Arti Tanda Dalam Matematika | Taqueria Autentica

apa arti tanda seru dalam matematika | Taqueria Autentica