De dans van sinus en cosinus: wanneer wordt hun som een half?
Stel je een cirkel voor, perfect rond en elegant. In deze cirkel bewegen twee dansers, sinus en cosinus, in een eeuwige wals. Ze draaien en buigen, hun bewegingen weergegeven door golvende lijnen. Op bepaalde magische momenten komen ze samen, hun krachten bundelen ze zich, en hun som wordt precies 1/2. Deze bijzondere ontmoeting, waar sin x + cos x = 1/2, is een bron van fascinatie voor wiskundigen en natuurkundigen.
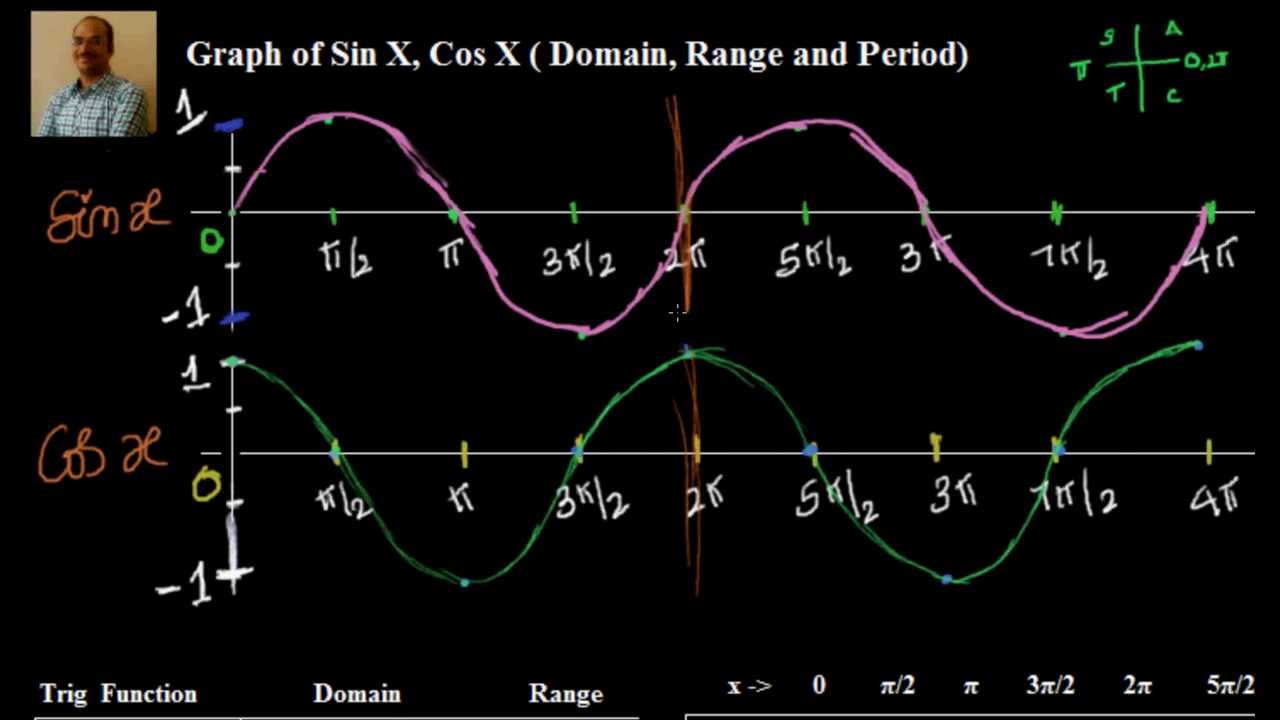
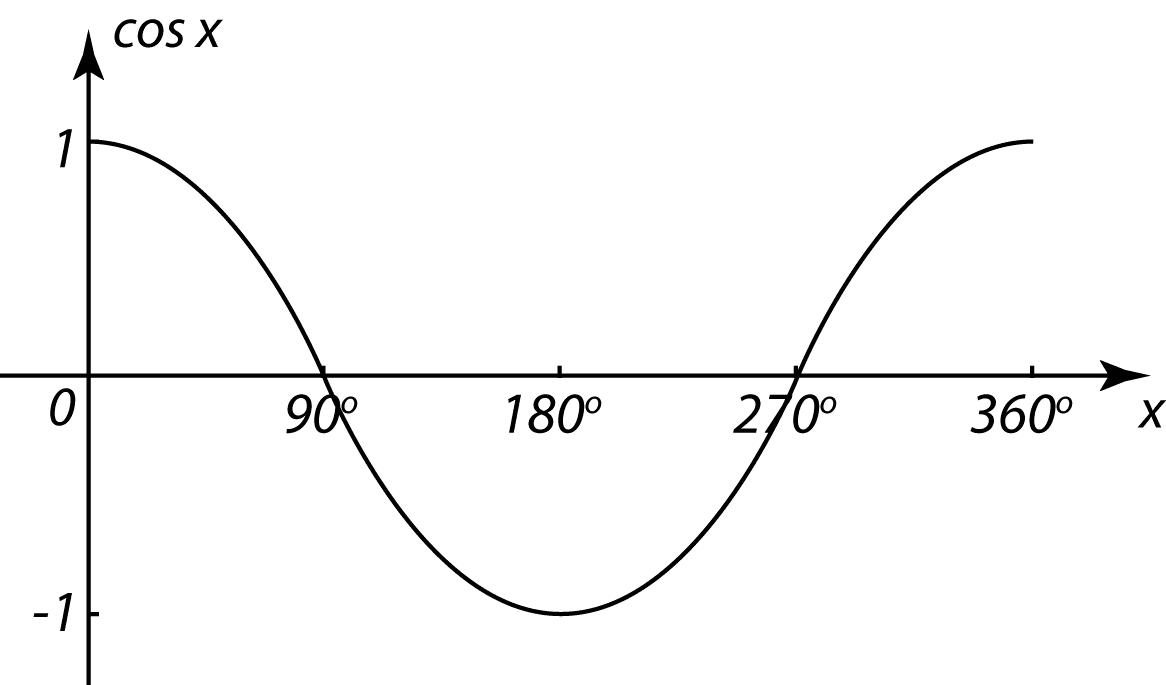
Maar wat betekent deze vergelijking nu precies? Sin x en cos x vertegenwoordigen de verhoudingen in een rechthoekige driehoek, gedefinieerd door een hoek x. Sin x is de overstaande zijde gedeeld door de schuine zijde, terwijl cos x de aanliggende zijde gedeeld door de schuine zijde is. Wanneer we zoeken naar de hoek x waarbij sin x + cos x = 1/2, zoeken we eigenlijk naar de specifieke vorm van een rechthoekige driehoek die aan deze voorwaarde voldoet.
De vergelijking sin x + cos x = 1/2 heeft wortels in de trigonometrie, een tak van de wiskunde die zich bezighoudt met de relaties tussen hoeken en zijden van driehoeken. Trigonometrie is al eeuwenlang een essentieel instrument in de astronomie, navigatie, muziek en architectuur. In de moderne tijd speelt het een cruciale rol in vakgebieden als natuurkunde, engineering en computergraphics.
Een manier om de oplossingen voor de vergelijking sin x + cos x = 1/2 te vinden, is door gebruik te maken van de trigonometrische identiteit sin(x + π/4) = (√2)/2 * (sin x + cos x). Door deze identiteit te gebruiken, kunnen we de vergelijking herschrijven als sin(x + π/4) = (√2)/4. De oplossingen voor deze vergelijking zijn x = -π/4 + 2πk of x = 3π/4 + 2πk, waarbij k een geheel getal is.
De vergelijking sin x + cos x = 1/2 heeft interessante toepassingen in verschillende vakgebieden. In de fysica kan deze vergelijking bijvoorbeeld opduiken bij het analyseren van golven, zoals lichtgolven of geluidsgolven. In de elektronica kan het relevant zijn bij het bestuderen van wisselstroomcircuits. En in de informatica kan het worden gebruikt bij computergraphics en beeldverwerking.
De pracht en de beperkingen van sin x + cos x = 1/2
Zoals elke wiskundige vergelijking heeft sin x + cos x = 1/2 zijn eigen voordelen en beperkingen. Laten we eens kijken:
| Voordelen | Beperkingen |
|---|---|
| Elegant en eenvoudig te begrijpen | Kan complex worden bij het oplossen voor specifieke waarden van x |
| Toepasbaar in verschillende vakgebieden | Vereist kennis van trigonometrie om volledig te begrijpen |
Hoewel het oplossen van de vergelijking sin x + cos x = 1/2 uitdagend kan zijn, is het een waardevolle oefening die ons begrip van trigonometrie en zijn toepassingen in de echte wereld verdiept. De dans van sinus en cosinus, met hun elegante bewegingen en verrassende ontmoetingen, blijft ons inspireren en uitdagen.

sin x + cos x 1/2 | Taqueria Autentica

sin x + cos x 1/2 | Taqueria Autentica

sin x + cos x 1/2 | Taqueria Autentica

sin x + cos x 1/2 | Taqueria Autentica

sin x + cos x 1/2 | Taqueria Autentica

sin x + cos x 1/2 | Taqueria Autentica

sin x + cos x 1/2 | Taqueria Autentica

sin x + cos x 1/2 | Taqueria Autentica

sin x + cos x 1/2 | Taqueria Autentica

sin x + cos x 1/2 | Taqueria Autentica
Given Sinx 0.5 What Is Cosx | Taqueria Autentica

sin x + cos x 1/2 | Taqueria Autentica

sin x + cos x 1/2 | Taqueria Autentica
Graphing Sine And Cosine Graphs | Taqueria Autentica

Gcse Exam Question Practice Sine And Cosine Rule | Taqueria Autentica