De mysterieuze wereld van ln(x) = 0 ontrafelen
Stel je voor: een wereld waarin getallen dansen en wiskundige vergelijkingen de sleutel vormen tot het ontsluiten van verborgen waarheden. In deze wereld stuiten we op een raadselachtige vergelijking: ln(x) = 0. Wat betekent dit? Hoe lossen we het op? En wat zijn de implicaties van de oplossing? Maak je klaar voor een fascinerende reis door de wereld van logaritmen, terwijl we de mysterieuze vergelijking ln(x) = 0 ontrafelen.
Laten we beginnen met het begrijpen van de spelers in deze vergelijking. De afkorting "ln" staat voor de natuurlijke logaritme. Een logaritme beantwoordt de vraag: "Tot welke macht moet ik een basis verheffen om een bepaald getal te krijgen?". In het geval van de natuurlijke logaritme is de basis het getal 'e', een irrationeel getal dat ongeveer gelijk is aan 2,71828. Dus, ln(x) = 0 vraagt: "Tot welke macht moet ik 'e' verheffen om 1 te krijgen?".
Het antwoord ligt in de eigenschappen van exponenten. Elk getal verheven tot de macht 0 is gelijk aan 1. Daarom is de oplossing van ln(x) = 0 simpelweg x = 1. De natuurlijke logaritme van 1 is 0, omdat e⁰ = 1.
Maar waarom is dit belangrijk? Logaritmen, inclusief de natuurlijke logaritme, spelen een cruciale rol in verschillende wetenschappelijke disciplines. Ze worden gebruikt om exponentiële groei en verval te modelleren, complexe berekeningen te vereenvoudigen en te helpen bij het oplossen van differentiaalvergelijkingen.
Stel je voor dat je de groei van een bacteriepopulatie bestudeert die exponentieel toeneemt. De natuurlijke logaritme kan worden gebruikt om de tijd te bepalen die nodig is om een bepaalde populatiegrootte te bereiken. In de financiële wereld worden logaritmen gebruikt om rente op rente te berekenen en investeringsgroei te voorspellen.
Het begrijpen van logaritmen en het kunnen oplossen van vergelijkingen zoals ln(x) = 0 is essentieel voor studenten, wetenschappers, ingenieurs en iedereen die te maken krijgt met wiskundige modellering en analyse.
Laten we, om de kracht van logaritmen verder te illustreren, eens kijken naar enkele praktische voorbeelden:
- Bepaling van de pH-waarde van een oplossing: de pH-waarde is een maat voor de zuurgraad of basiciteit van een oplossing en wordt berekend met behulp van een logaritmische schaal.
- Het meten van de intensiteit van aardbevingen: de schaal van Richter, die de kracht van aardbevingen meet, is een logaritmische schaal.
- Het berekenen van de halveringstijd van radioactief materiaal: de halveringstijd, de tijd die nodig is om de helft van een hoeveelheid radioactief materiaal te laten vervallen, wordt berekend met behulp van logaritmen.
Deze voorbeelden laten zien dat logaritmen, en in het bijzonder de natuurlijke logaritme, onmisbare instrumenten zijn in ons begrip van de wereld om ons heen.
Dus, de volgende keer dat je de vergelijking ln(x) = 0 tegenkomt, herinner je dan de reis die we hebben gemaakt. Herinner je de elegantie en kracht van logaritmen, en waardeer de rol die ze spelen bij het ontrafelen van de mysteries van ons universum.

How to Change the Base of a Logarithm | Taqueria Autentica
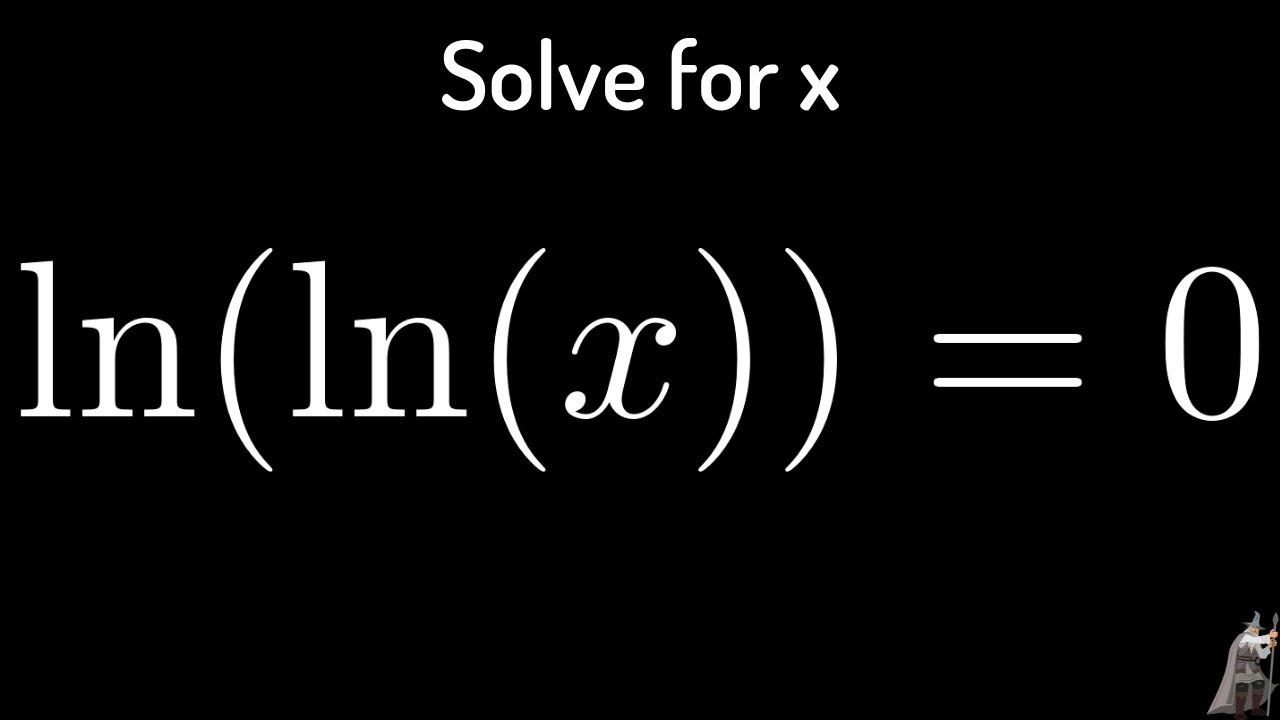
how to solve ln x 0 | Taqueria Autentica

how to solve ln x 0 | Taqueria Autentica

Verify that lnx=(ln10)(logx), and discuss w h y they're equal. Then use | Taqueria Autentica

how to solve ln x 0 | Taqueria Autentica

how to solve ln x 0 | Taqueria Autentica
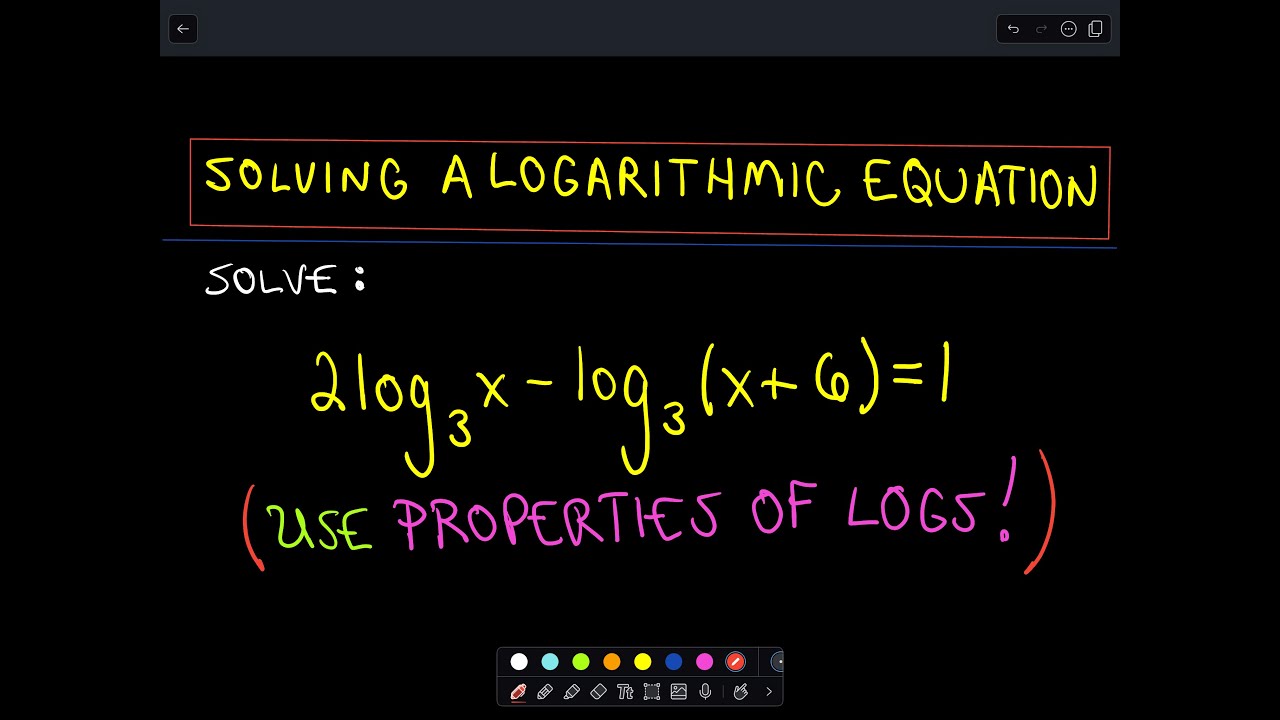
Logarithmic Equations Examples And Solutions | Taqueria Autentica

how to solve ln x 0 | Taqueria Autentica

how to solve ln x 0 | Taqueria Autentica

how to solve ln x 0 | Taqueria Autentica

how to solve ln x 0 | Taqueria Autentica

Natural Log Simplyifying With E Rules Clearance | Taqueria Autentica

how to solve ln x 0 | Taqueria Autentica

how to solve ln x 0 | Taqueria Autentica

Solving Equations Using Logarithms | Taqueria Autentica