De Oppervlakte van een Vijfhoek Berekenen: Een Praktische Gids

02 Sep 2024

Stel je voor: je bent een architect die een uniek gebouw ontwerpt, of misschien ben je een kunstenaar die geometrische patronen verkent. In beide gevallen kom je wellicht de vijfhoek tegen - een fascinerende vorm met vijf zijden die al eeuwenlang tot de verbeelding spreekt. Maar hoe bereken je eigenlijk de oppervlakte van deze intrigerende veelhoek?

Het begrijpen van de oppervlakte van een vijfhoek is niet alleen essentieel voor wiskundige problemen, maar ook voor praktische toepassingen in verschillende disciplines. In deze gids duiken we in de wereld van vijfhoeken, verkennen we de formules om hun oppervlakte te berekenen en ontdekken we de relevantie ervan in ons dagelijks leven.

Voordat we in de formules duiken, is het belangrijk om te begrijpen dat er verschillende soorten vijfhoeken zijn, waaronder regelmatige en onregelmatige vijfhoeken. Een regelmatige vijfhoek heeft vijf gelijke zijden en vijf gelijke hoeken, terwijl een onregelmatige vijfhoek zijden en hoeken van verschillende grootte kan hebben. De aanpak voor het berekenen van de oppervlakte verschilt enigszins, afhankelijk van het type vijfhoek.

De geschiedenis van de vijfhoek gaat terug tot de oude beschavingen. De Egyptenaren gebruikten de vijfhoek in hun architectuur, zoals te zien is in de constructie van de piramides. De Griekse wiskundigen bestudeerden de vijfhoek uitgebreid en ontdekten zijn unieke geometrische eigenschappen, waaronder de Gulden Snede, die een speciale verhouding vertegenwoordigt die in de natuur en kunst voorkomt.

Tegenwoordig speelt de vijfhoek een belangrijke rol in verschillende gebieden, waaronder architectuur, kunst en natuur. Denk bijvoorbeeld aan de vijfhoekige vorm van het Pentagon in de Verenigde Staten, het grootste kantoorgebouw ter wereld. In de natuur zien we de vijfhoekige vorm terug in de rangschikking van bloemblaadjes in sommige bloemen en de structuur van honingraten.

Voor- en nadelen van het Berekenen van de Oppervlakte van een Vijfhoek

Voordelen	Nadelen
Noodzakelijk voor praktische toepassingen in verschillende disciplines	Kan complex zijn voor onregelmatige vijfhoeken
Helpt bij het begrijpen van geometrische concepten	Vereist kennis van specifieke formules
Bevordert probleemoplossend denken	-

Veelgestelde Vragen over de Oppervlakte van een Vijfhoek

1. Wat is de formule voor de oppervlakte van een regelmatige vijfhoek?

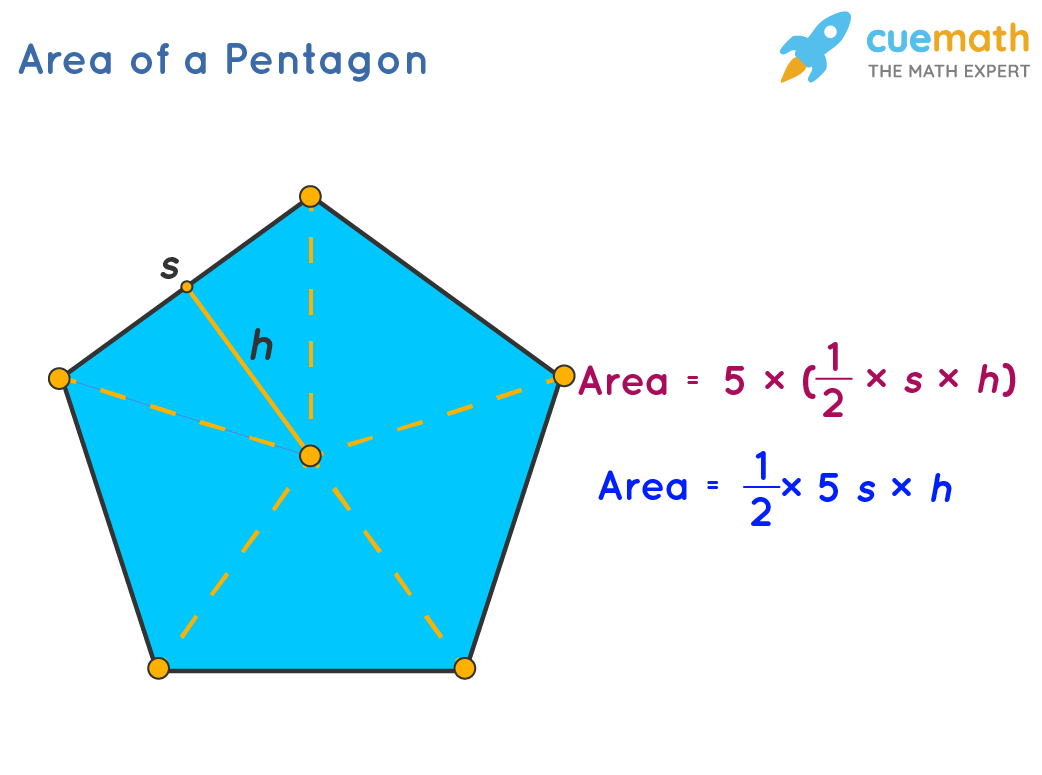
De formule voor de oppervlakte (A) van een regelmatige vijfhoek is: A = (5/4) * a² * cot(π/5), waarbij 'a' de lengte van een zijde is.

2. Hoe bereken ik de oppervlakte van een onregelmatige vijfhoek?

Voor onregelmatige vijfhoeken kun je de vijfhoek verdelen in kleinere vormen, zoals driehoeken, waarvan je de oppervlakte kunt berekenen en vervolgens optellen.

3. Waar kan ik meer informatie vinden over de vijfhoek en zijn eigenschappen?

Websites zoals Wikipedia en Wolfram MathWorld bieden gedetailleerde informatie over vijfhoeken.

4. Wat zijn enkele praktische toepassingen van het berekenen van de oppervlakte van een vijfhoek?

Praktische toepassingen zijn te vinden in de architectuur (bijvoorbeeld bij het ontwerpen van gebouwen met vijfhoekige vormen), de landmeetkunde (bijvoorbeeld bij het bepalen van de oppervlakte van een stuk land met een onregelmatige vorm) en de materiaalkunde (bijvoorbeeld bij het berekenen van de hoeveelheid materiaal die nodig is om een vijfhoekig object te maken).

5. Zijn er online tools beschikbaar om de oppervlakte van een vijfhoek te berekenen?

Ja, er zijn verschillende online calculators beschikbaar die de oppervlakte van een vijfhoek kunnen berekenen. Zoek gewoon naar "oppervlakte vijfhoek calculator" op Google.

6. Wat is de rol van de Gulden Snede in een vijfhoek?

De Gulden Snede, ongeveer gelijk aan 1.618, is nauw verbonden met de vijfhoek. De verhouding tussen de diagonaal en de zijde van een regelmatige vijfhoek is gelijk aan de Gulden Snede.

7. Kan ik de oppervlakte van een vijfhoek berekenen met alleen de lengte van de zijden?

Voor regelmatige vijfhoeken kun je de oppervlakte berekenen met alleen de lengte van de zijden. Voor onregelmatige vijfhoeken heb je echter meer informatie nodig, zoals de hoeken of de lengte van de diagonalen.

8. Wat zijn enkele veelvoorkomende fouten bij het berekenen van de oppervlakte van een vijfhoek?

Veelvoorkomende fouten zijn het gebruik van de verkeerde formule (bijvoorbeeld het gebruiken van de formule voor een regelmatige vijfhoek voor een onregelmatige vijfhoek) of het niet correct meten van de zijden of hoeken.

Conclusie

Het begrijpen van de oppervlakte van een vijfhoek is een fundamenteel concept in de meetkunde dat praktische toepassingen heeft in verschillende disciplines. Of je nu een student, professional of gewoon nieuwsgierig bent, het kennen van de formules en methoden om de oppervlakte van een vijfhoek te berekenen kan nuttig zijn in verschillende situaties. Van architectuur tot natuur, de vijfhoek is een fascinerende vorm met een rijke geschiedenis en praktische relevantie in ons dagelijks leven.