Hellingsgetal Berekenen De Ultieme Gids
Hoe steil is die heuvel? Hoe snel stijgt die grafiek? Het hellingsgetal geeft antwoord op deze vragen. Het is een essentieel concept in de wiskunde en heeft talloze toepassingen in de praktijk, van het ontwerpen van wegen tot het analyseren van financiële trends.
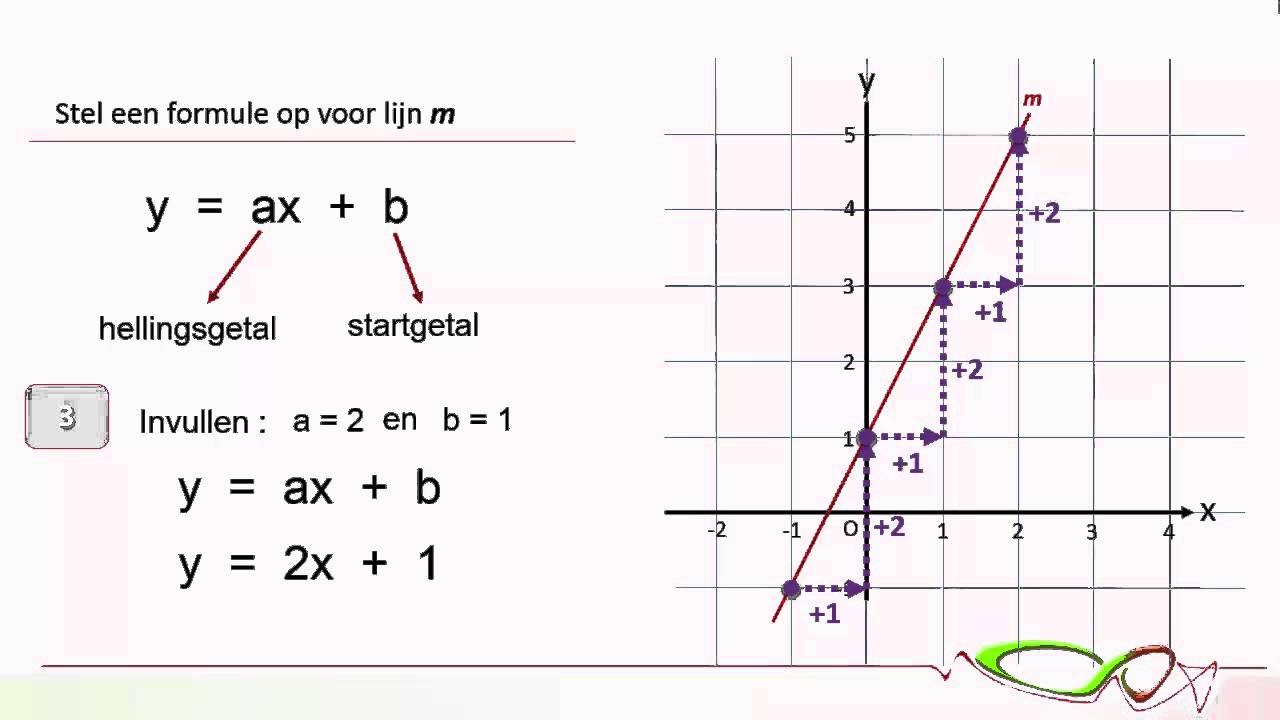
Het bepalen van de helling van een lijn, oftewel het hellingsgetal berekenen, is een fundamentele vaardigheid in de wiskunde. Het hellingsgetal vertegenwoordigt de verandering in de verticale richting ten opzichte van de verandering in de horizontale richting. Simpel gezegd: hoe groter het hellingsgetal, hoe steiler de lijn.
Maar hoe bereken je dit getal precies? Er zijn verschillende methoden om het hellingsgetal te vinden, afhankelijk van de beschikbare informatie. Heb je twee punten op de lijn? Dan kun je de formule (y2 - y1) / (x2 - x1) gebruiken. Is de vergelijking van de lijn gegeven in de vorm y = mx + b? Dan is het hellingsgetal simpelweg de waarde van 'm'.
De geschiedenis van het hellingsgetal is verweven met de ontwikkeling van de analytische meetkunde. Wiskundigen zoals René Descartes en Pierre de Fermat legden de basis voor dit concept, wat ons in staat stelt om geometrische figuren met algebraïsche vergelijkingen te beschrijven. Het hellingsgetal speelt een cruciale rol in deze beschrijving.
Het belang van het hellingsgetal reikt verder dan de wiskundeles. In de natuurkunde beschrijft het de snelheid van verandering, bijvoorbeeld de snelheid van een bewegend object. In de economie geeft het de mate van verandering in een economische variabele aan. In de architectuur is het essentieel voor het ontwerpen van daken en hellingen. Kortom, het hellingsgetal is een krachtig instrument om de wereld om ons heen te begrijpen en te modelleren.
De formule voor het hellingsgetal, gegeven twee punten (x1, y1) en (x2, y2), is: (y2 - y1) / (x2 - x1). Stel, je hebt de punten (1, 2) en (4, 8). Het hellingsgetal is dan (8 - 2) / (4 - 1) = 6 / 3 = 2.
Voordelen van het begrijpen van het hellingsgetal:
1. Visualiseren van trends: Door het hellingsgetal te berekenen, kun je de trend van een dataset visualiseren en interpreteren.
2. Voorspellingen maken: Met behulp van het hellingsgetal kun je voorspellingen doen over toekomstige waarden, bijvoorbeeld de toekomstige groei van een bedrijf.
3. Problemen oplossen: Het hellingsgetal helpt bij het oplossen van praktische problemen, zoals het bepalen van de optimale hoek voor een dak.
Stap-voor-stap handleiding:
1. Identificeer twee punten op de lijn.
2. Bepaal de x- en y-coördinaten van elk punt.
3. Pas de formule (y2 - y1) / (x2 - x1) toe.
Voor- en Nadelen
| Voordeel | Nadeel |
|---|---|
| Helpt bij het begrijpen van verandering | Kan complex zijn voor niet-lineaire functies |
Veelgestelde vragen:
1. Wat is het hellingsgetal? Het hellingsgetal is de mate van steilheid van een lijn.
2. Hoe bereken je het hellingsgetal? Met de formule (y2 - y1) / (x2 - x1) of door de 'm' in y = mx + b te vinden.
3. Wat betekent een negatief hellingsgetal? Een dalende lijn.
4. Wat betekent een hellingsgetal van 0? Een horizontale lijn.
5. Wat betekent een oneindig hellingsgetal? Een verticale lijn.
6. Waar wordt het hellingsgetal gebruikt? In wiskunde, natuurkunde, economie, architectuur, etc.
7. Hoe interpreteer je het hellingsgetal? Een groter getal betekent een steilere lijn.
8. Wat is het verschil tussen hellingsgetal en richtingscoëfficiënt? Deze termen zijn synoniemen.
Tip: Oefening baart kunst! Hoe meer je oefent met het berekenen van het hellingsgetal, hoe beter je het zult begrijpen.
Het hellingsgetal is een krachtig instrument om de wereld om ons heen te begrijpen. Van het beschrijven van de steilheid van een helling tot het analyseren van complexe datasets, het hellingsgetal speelt een cruciale rol in diverse disciplines. Door de formules en concepten achter het hellingsgetal te beheersen, kunnen we inzicht krijgen in trends, voorspellingen doen en problemen oplossen. Of je nu student, wetenschapper of gewoon nieuwsgierig bent, het begrijpen van het hellingsgetal opent de deur naar een dieper begrip van de wereld. Verken de mogelijkheden en ontdek de kracht van het hellingsgetal!

Voorkennis Wiskunde Les 8 Hoofdstuk 3 33 34 en ppt download | Taqueria Autentica

Wat Zijn Variabele Kosten Voor Een Bedrijf | Taqueria Autentica
Wiskunde Hoe Maak Ik Een Tabel En Een Grafiek Bij Een Lineaire Formule | Taqueria Autentica

Hoe bereken je de terugverdientijd van zonnepanelen | Taqueria Autentica

Hoe moet je Ampere berekenen | Taqueria Autentica

Wat zijn natuurlijke getallen | Taqueria Autentica

Hoe bereken je de terugverdientijd van zonnepanelen | Taqueria Autentica

hoe bereken je hellingsgetal | Taqueria Autentica

Hoe bereken je de terugverdientijd van zonnepanelen | Taqueria Autentica

Transitievergoeding wanneer heeft de werknemer er recht op en hoe | Taqueria Autentica

Thema Lineair verband 1 GRAFIEK TABEL FORMULE 2 | Taqueria Autentica

Hoe bereken je een bruto jaarinkomen berekenen voor de bank | Taqueria Autentica
Hoe Bereken Je Wettelijke Rente | Taqueria Autentica

Hoe Bereken je Netto Bijtelling Lease Auto | Taqueria Autentica
Hoe Bereken Je Vierkante Meter | Taqueria Autentica