Hoeken in een Driehoek Berekenen Ontdek de Geheimen
Driehoeken, die ogenschijnlijk eenvoudige geometrische figuren, vormen de basis van talloze constructies en ontwerpen. Maar hoe bepalen we de hoeken binnen deze driehoeken? Het berekenen van hoeken in een driehoek is essentieel in vakgebieden zoals architectuur, engineering, natuurkunde en zelfs kunst. Dit artikel duikt in de wereld van driehoekshoeken en biedt een uitgebreide gids voor het bepalen van hun waarden.
Van het bepalen van de hoogte van een gebouw tot het ontwerpen van een brug, de kennis van driehoekshoeken is onmisbaar. Stel je voor dat je een dak wilt bouwen: de hoek van de helling is cruciaal voor de stabiliteit en functionaliteit. Of denk aan navigatie, waarbij de positiebepaling vaak gebaseerd is op driehoeksberekeningen. Het beheersen van deze vaardigheid opent deuren naar een beter begrip van de wereld om ons heen.
De geschiedenis van het berekenen van hoeken in driehoeken gaat terug tot de oude Grieken, met name tot de werken van Euclides. Zijn baanbrekende werk, de Elementen, legde de fundamenten voor de geometrie zoals we die vandaag kennen. De stelling van Pythagoras, een essentieel instrument voor het berekenen van zijden en indirect ook hoeken in rechthoekige driehoeken, is een bekend voorbeeld van deze oude kennis.
Het belang van het correct bepalen van driehoekshoeken kan niet genoeg benadrukt worden. Fouten in deze berekeningen kunnen leiden tot structurele instabiliteit in gebouwen, onnauwkeurige navigatie en problemen in talloze andere toepassingen. Daarom is een grondig begrip van de verschillende methoden en technieken essentieel.
Verschillende methoden staan tot onze beschikking om driehoekshoeken te berekenen. De hoekensom van een driehoek is altijd 180 graden. Als twee hoeken bekend zijn, kan de derde hoek eenvoudig berekend worden. Voor rechthoekige driehoeken kunnen we de goniometrische functies sinus, cosinus en tangens gebruiken. De sinusregel en cosinusregel bieden oplossingen voor niet-rechthoekige driehoeken.
Voorbeeld: In een rechthoekige driehoek met een hoek van 30 graden en een rechte hoek (90 graden), is de derde hoek 180 - 90 - 30 = 60 graden.
Voor- en Nadelen van Hoeken Berekenen
| Voordelen | Nadelen |
|---|---|
| Essentieel voor ontwerp en constructie | Vereist nauwkeurigheid om fouten te vermijden |
| Fundamenteel voor navigatie en positionering | Kan complex zijn bij niet-rechthoekige driehoeken |
| Basis voor veel wiskundige en wetenschappelijke concepten | Verschillende methoden vereisen verschillende aanpakken |
Veelgestelde vragen:
1. Wat is de som van de hoeken in een driehoek? Antwoord: 180 graden.
2. Hoe bereken ik de derde hoek als ik twee hoeken ken? Antwoord: Trek de twee bekende hoeken af van 180 graden.
3. Wat is de stelling van Pythagoras? Antwoord: a² + b² = c², waarbij a en b de rechthoekszijden zijn en c de schuine zijde.
4. Wanneer gebruik ik de sinusregel? Antwoord: Bij niet-rechthoekige driehoeken wanneer je een hoek en de tegenoverliggende zijde kent, en nog een zijde of hoek.
5. Wanneer gebruik ik de cosinusregel? Antwoord: Bij niet-rechthoekige driehoeken wanneer je twee zijden en de ingesloten hoek kent, of drie zijden.
6. Wat zijn goniometrische functies? Antwoord: Relaties tussen hoeken en zijden van een rechthoekige driehoek (sinus, cosinus, tangens).
7. Hoe bereken ik de hoek van een helling? Antwoord: Gebruik de tangens van de hoek, die gelijk is aan de overstaande zijde gedeeld door de aanliggende zijde.
8. Waar kan ik meer informatie vinden over hoeken berekenen in een driehoek? Antwoord: Online bronnen, wiskundeboeken en educatieve apps.
Tips en Trucs: Maak altijd een schets van de driehoek. Label de zijden en hoeken duidelijk. Kies de juiste formule op basis van de gegeven informatie.
Het berekenen van hoeken in een driehoek is een fundamentele vaardigheid met brede toepassingen. Van architectuur tot navigatie, het beheersen van deze techniek is essentieel voor succes in diverse disciplines. Door de verschillende methoden te begrijpen en toe te passen, kunnen we de geheimen van driehoeken ontsluiten en hun kracht benutten in ons dagelijks leven. Door te oefenen met verschillende voorbeelden en de theorie te bestuderen, kun je je vaardigheden in het berekenen van hoeken in een driehoek verder ontwikkelen en de basis leggen voor toekomstig succes in wiskunde en aanverwante vakgebieden. Het is een vaardigheid die de moeite waard is om te leren en die je gedurende je hele academische en professionele carrière van dienst zal zijn.

hoeken berekenen in een driehoek | Taqueria Autentica

Hoeken berekenen binnen een driehoek | Taqueria Autentica
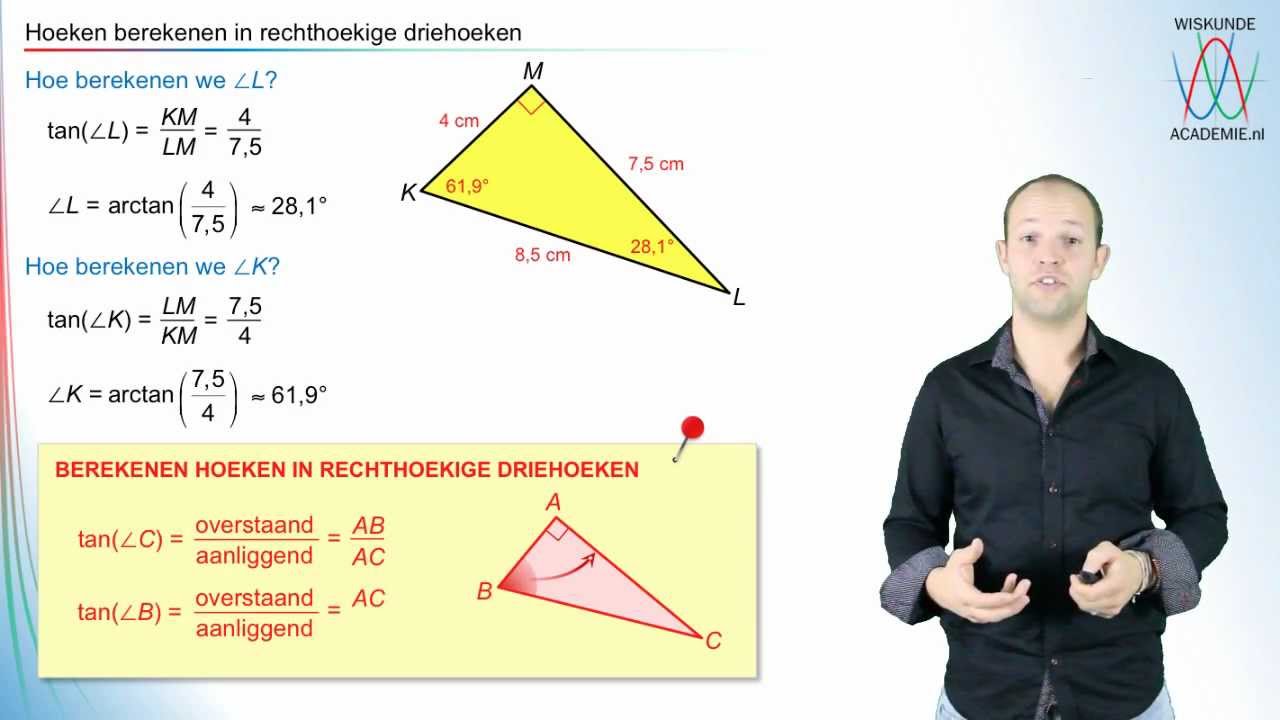
Zijde Driehoek Berekenen Zonder Rechte Hoek Eenvoudige Methoden Uitgelegd | Taqueria Autentica

Zijde Driehoek Berekenen Zonder Rechte Hoek Eenvoudige Methoden Uitgelegd | Taqueria Autentica

Hoeken berekenen in driehoeken | Taqueria Autentica
som van de hoeken van een driehoek | Taqueria Autentica

hoeken berekenen in een driehoek | Taqueria Autentica

De hoeken in een driehoek | Taqueria Autentica

hoeken berekenen in een driehoek | Taqueria Autentica

Hoe Bereken Je Een Vierkante Meter | Taqueria Autentica

hoeken berekenen in een driehoek | Taqueria Autentica

hoeken berekenen in een driehoek | Taqueria Autentica

Hoeken berekenen binnen een driehoek | Taqueria Autentica

Hoeken berekenen binnen een driehoek | Taqueria Autentica
Parameters berekenen van een rechte driehoek met hoeken 45 45 90 | Taqueria Autentica