Negatieve getallen beheersen: Rekenoperaties en praktische toepassingen
Stel je voor: je banksaldo duikt onder nul. De temperatuur daalt onder het vriespunt. Of je telt af voor een raketlancering. Wat hebben deze scenario's gemeen? Negatieve getallen! Ze spelen een cruciale rol in ons dagelijks leven en in diverse vakgebieden, van financiën tot wetenschap. Maar hoe reken je er eigenlijk mee? Deze gids biedt een helder overzicht van de basisprincipes en praktische toepassingen van negatieve getallen.
Het begrijpen van negatieve getallen is essentieel voor het oplossen van talloze problemen. Of je nu je financiën beheert, een natuurkundig experiment uitvoert of een computerprogramma schrijft, de kans is groot dat je negatieve getallen tegenkomt. Deze handleiding duikt in de wereld van negatieve getallen, van de basisregels tot meer complexe berekeningen.
Negatieve getallen vertegenwoordigen waarden kleiner dan nul. Ze worden aangegeven met een minteken (-) voor het getal, bijvoorbeeld -5 of -10. In tegenstelling tot positieve getallen, die een toename of een hoeveelheid boven nul aangeven, drukken negatieve getallen een afname, een tekort of een waarde onder nul uit. Denk bijvoorbeeld aan een schuld als een negatief getal, terwijl een tegoed positief is.
Rekenen met negatieve getallen kan in het begin verwarrend lijken, maar met de juiste uitleg en oefening wordt het al snel een tweede natuur. De belangrijkste regels voor optellen, aftrekken, vermenigvuldigen en delen worden in deze gids stapsgewijs uitgelegd, aangevuld met praktische voorbeelden en tips.
De geschiedenis van negatieve getallen gaat ver terug. Hoewel ze in eerste instantie met scepsis werden bekeken, werden ze uiteindelijk geaccepteerd als essentiële wiskundige concepten. In de moderne wiskunde spelen negatieve getallen een onmisbare rol in algebra, calculus en andere disciplines.
Optellen en aftrekken: Stel je voor dat je -5 euro schuld hebt en je leent nog eens 3 euro. Je totale schuld wordt dan -8 euro (-5 + -3 = -8). Aftrekken van een negatief getal is hetzelfde als optellen van het positieve equivalent. Dus, -5 - -3 is hetzelfde als -5 + 3, wat resulteert in -2.
Vermenigvuldigen en delen: Bij het vermenigvuldigen of delen van twee negatieve getallen is de uitkomst altijd positief. Bijvoorbeeld, -5 x -3 = 15 en -10 / -2 = 5. Als je een negatief getal vermenigvuldigt of deelt met een positief getal, is de uitkomst negatief.
Voordelen van het begrijpen van negatieve getallen:
1. Financiën beheren: Negatieve getallen helpen bij het begrijpen van schulden, kredieten en budgettering.
2. Wetenschappelijke berekeningen: Negatieve getallen zijn essentieel in natuurkunde, scheikunde en andere wetenschappen.
3. Data-analyse: Negatieve getallen spelen een rol bij het analyseren van trends en veranderingen.
Veelgestelde vragen:
1. Wat is een negatief getal? Een getal kleiner dan nul.
2. Hoe tel je twee negatieve getallen op? Tel de absolute waarden op en plaats een minteken ervoor.
3. Hoe trek je een negatief getal af? Tel het positieve equivalent op.
4. Wat is het resultaat van het vermenigvuldigen van twee negatieve getallen? Een positief getal.
5. Wat is het resultaat van het delen van een negatief getal door een positief getal? Een negatief getal.
6. Waar worden negatieve getallen gebruikt? In financiën, wetenschap, data-analyse, enz.
7. Hoe kan ik beter worden in rekenen met negatieve getallen? Door te oefenen met diverse opgaven.
8. Zijn er online bronnen beschikbaar om negatieve getallen te leren? Ja, er zijn veel websites en apps die hulp bieden.
Tips en trucs: Gebruik een getallenlijn om negatieve getallen te visualiseren. Oefen regelmatig met verschillende rekenopgaven. Zoek online naar extra oefeningen en uitleg.
Het beheersen van negatieve getallen is een essentiële vaardigheid voor iedereen. Of je nu je persoonlijke financiën beheert, wetenschappelijke berekeningen uitvoert of simpelweg de dagelijkse temperatuur wilt begrijpen, negatieve getallen spelen een cruciale rol. Door de basisregels te begrijpen en regelmatig te oefenen, kun je met vertrouwen rekenen met negatieve getallen en hun toepassingen in de wereld om je heen waarderen. Investeer tijd in het leren over negatieve getallen en ontdek hoe ze je begrip van wiskunde en de wereld kunnen verdiepen. Vergeet niet: oefening baart kunst. Blijf oefenen en je zult zien dat negatieve getallen steeds minder intimiderend worden en steeds meer een waardevol hulpmiddel in je wiskundige toolkit.

Hoe Bereken Je Een Gemiddelde De Simpele Stappen | Taqueria Autentica

Machten met Negatieve Gebroken Exponenten | Taqueria Autentica

Spring Consulting Wat doe jij met je negatieve gedachten | Taqueria Autentica

hoe reken je negatieve getallen uit | Taqueria Autentica

hoe reken je negatieve getallen uit | Taqueria Autentica
Hoe Bereken Je Het Gemiddeld Eigen Vermogen | Taqueria Autentica

Op dit werkblad reken je uit hoeveel de getallen samen zijn Op dit | Taqueria Autentica

hoe reken je negatieve getallen uit | Taqueria Autentica
Samenvatting van Getallen uit Rekenen voor groep 7 | Taqueria Autentica

hoe reken je negatieve getallen uit | Taqueria Autentica

Werkbladen Rekenen Groep 8 Voor Scholen En Rt Aandacht Voor Rekenen | Taqueria Autentica

Hoe Reken Je Korting Uit Eenvoudige Stappen Voor Besparingen | Taqueria Autentica
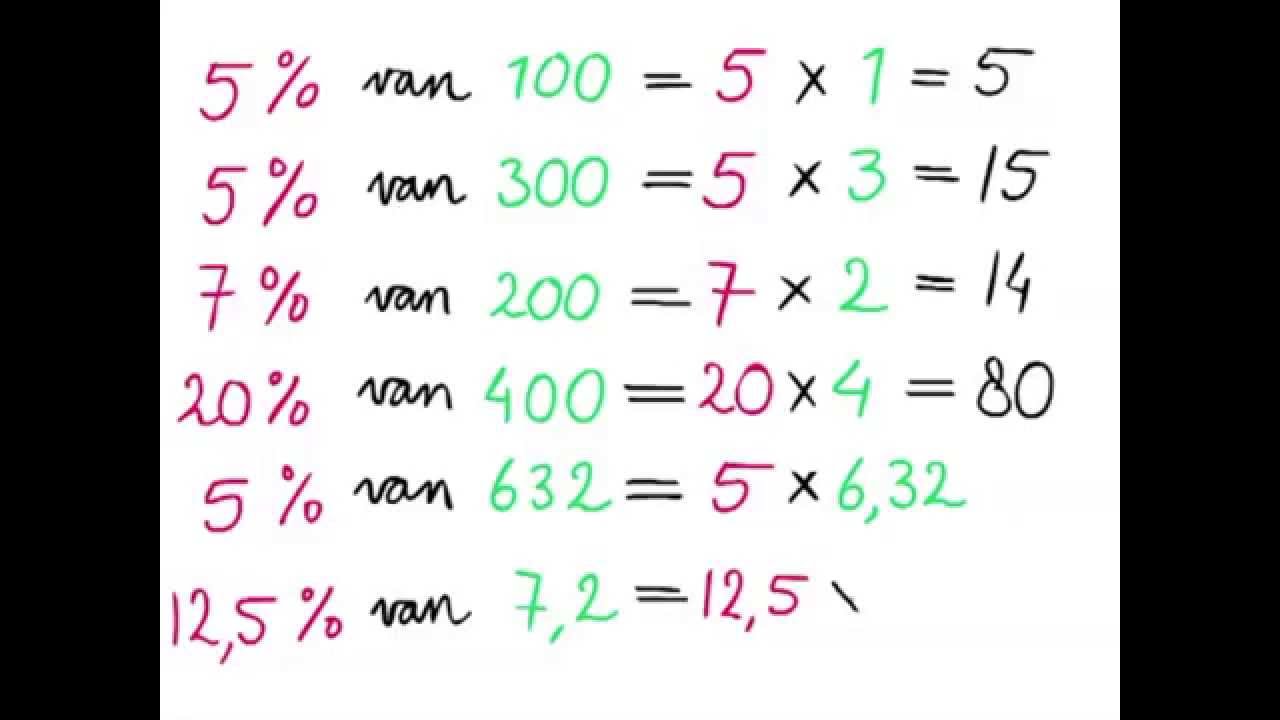
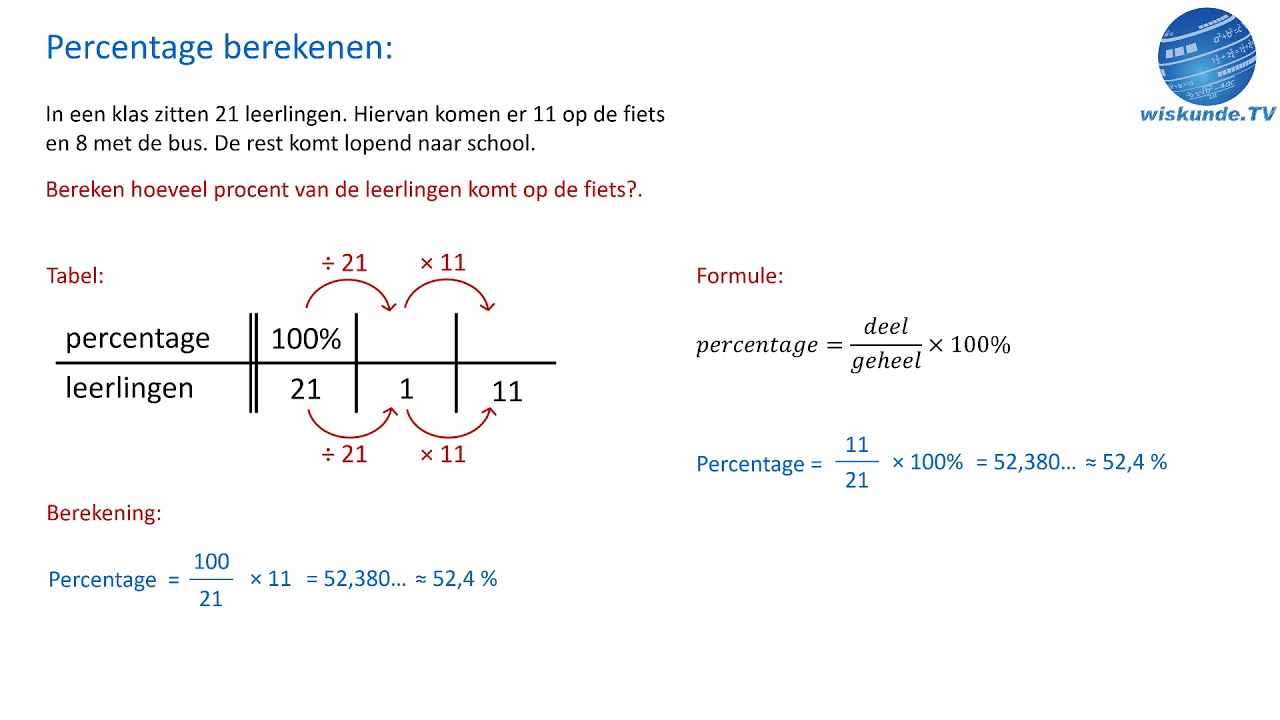
Hoe Reken Ik Procenten Uit Een Handige Gids Voor Beginners | Taqueria Autentica

hoe reken je negatieve getallen uit | Taqueria Autentica

Rekenblad Kies het goede teken 3 | Taqueria Autentica