Rechthoekige Driehoek Berekenen Ontdek de Geheimen
Hoe meet je de wereld om je heen? Van architectuur tot navigatie, de rechthoekige driehoek speelt een cruciale rol. Het begrijpen van de berekeningen achter deze geometrische vorm opent deuren naar een dieper begrip van wiskunde en de wereld om ons heen. Deze gids duikt diep in de wereld van de rechthoekige driehoek, van de basisprincipes tot geavanceerde technieken.
De rechthoekige driehoek, gedefinieerd door zijn kenmerkende rechte hoek, is meer dan alleen een vorm. Het is een bouwsteen in talloze disciplines. Of je nu de hoogte van een gebouw wilt berekenen, de afstand tot een ster wilt schatten of een complex technisch probleem wilt oplossen, de kennis van hoe je een rechthoekige driehoek berekent is essentieel.
Het berekenen van een rechthoekige driehoek draait om het vinden van de onbekende zijden en hoeken. De stelling van Pythagoras, een fundamenteel concept in de geometrie, vormt de basis voor veel van deze berekeningen. Deze stelling stelt dat in een rechthoekige driehoek het kwadraat van de lengte van de schuine zijde (de zijde tegenover de rechte hoek) gelijk is aan de som van de kwadraten van de lengtes van de twee andere zijden (de rechthoekszijden).
Naast de stelling van Pythagoras spelen ook trigonometrische functies zoals sinus, cosinus en tangens een belangrijke rol bij het berekenen van rechthoekige driehoeken. Deze functies relateren de hoeken van een driehoek aan de verhoudingen van de lengtes van de zijden. Door deze functies te gebruiken, kunnen we onbekende zijden en hoeken berekenen, zelfs als we slechts beperkte informatie hebben.
De geschiedenis van het berekenen van rechthoekige driehoeken gaat terug tot de oude beschavingen. De Babyloniërs en Egyptenaren gebruikten deze kennis voor landmeting, bouwprojecten en astronomie. De Griekse wiskundige Pythagoras formaliseerde de stelling die zijn naam draagt, waardoor een solide basis werd gelegd voor toekomstige wiskundige ontwikkelingen.
Voorbeelden van berekeningen:
1. Een rechthoekige driehoek heeft rechthoekszijden van 3 en 4 cm. Bereken de schuine zijde: 3² + 4² = c² => c = 5 cm.
2. Een rechthoekige driehoek heeft een hoek van 30 graden en een overstaande zijde van 5 cm. Bereken de aanliggende zijde met behulp van de tangens.
3. Een rechthoekige driehoek heeft een schuine zijde van 10 cm en een hoek van 60 graden. Bereken de overstaande zijde met behulp van de sinus.
Voordelen van het begrijpen van rechthoekige driehoeken:
1. Probleemoplossing: Vanuit het berekenen van afstanden tot het ontwerpen van structuren, de principes van rechthoekige driehoeken zijn overal toepasbaar.
2. Ruimtelijk inzicht: Het werken met rechthoekige driehoeken verbetert het begrip van ruimtelijke relaties.
3. Fundament voor wiskunde: Het beheersen van deze concepten legt een solide basis voor meer geavanceerde wiskundige onderwerpen.
Tips en Trucs:
Maak altijd een schets van de driehoek en label de zijden en hoeken.
Zorg ervoor dat je de juiste trigonometrische functie gebruikt.
FAQ:
1. Wat is de stelling van Pythagoras? Antwoord: a² + b² = c²
2. Wat is sinus? Antwoord: overstaande zijde / schuine zijde
3. Wat is cosinus? Antwoord: aanliggende zijde / schuine zijde
4. Wat is tangens? Antwoord: overstaande zijde / aanliggende zijde
5. Hoe vind ik de hoek als ik twee zijden ken? Antwoord: Gebruik de inverse trigonometrische functies.
6. Wat is een rechthoekszijde? Antwoord: De zijden die de rechte hoek vormen.
7. Wat is de schuine zijde? Antwoord: De zijde tegenover de rechte hoek.
8. Waar kan ik meer informatie vinden over trigonometrie? Antwoord: Kijk online naar bronnen of raadpleeg een wiskundeboek.
Kortom, het begrijpen van hoe je een rechthoekige driehoek berekent is een essentiële vaardigheid met brede toepassingen. Van het oplossen van alledaagse problemen tot het verkennen van complexe wetenschappelijke concepten, de principes van de rechthoekige driehoek vormen een krachtig hulpmiddel. Door de stelling van Pythagoras en trigonometrische functies te beheersen, kunnen we de wereld om ons heen beter begrijpen en waarderen. Door te blijven oefenen en te verkennen, kunnen we de ware kracht van deze fundamentele geometrische vorm ontsluiten. Neem de tijd om te oefenen met verschillende voorbeelden en verken de vele online bronnen die beschikbaar zijn. Het beheersen van deze vaardigheid opent de deur naar een wereld van mogelijkheden.

De richtingscoëfficiënt of rico | Taqueria Autentica

hoe bereken je een rechthoekige driehoek | Taqueria Autentica

Hoe Bereken Je De Oppervlakte Van Een Rechthoek Een Simpele Gids | Taqueria Autentica
Verschillende soorten driehoeken en het berekenen van de hoeken oefenen | Taqueria Autentica

hoe bereken je een rechthoekige driehoek | Taqueria Autentica

hoe bereken je een rechthoekige driehoek | Taqueria Autentica

hoe bereken je een rechthoekige driehoek | Taqueria Autentica

hoe bereken je een rechthoekige driehoek | Taqueria Autentica

Hoe Bereken Je De Oppervlakte Van Een Driehoek Simpele Uitleg En Formule | Taqueria Autentica

hoe bereken je een rechthoekige driehoek | Taqueria Autentica

hoe bereken je een rechthoekige driehoek | Taqueria Autentica

hoe bereken je een rechthoekige driehoek | Taqueria Autentica
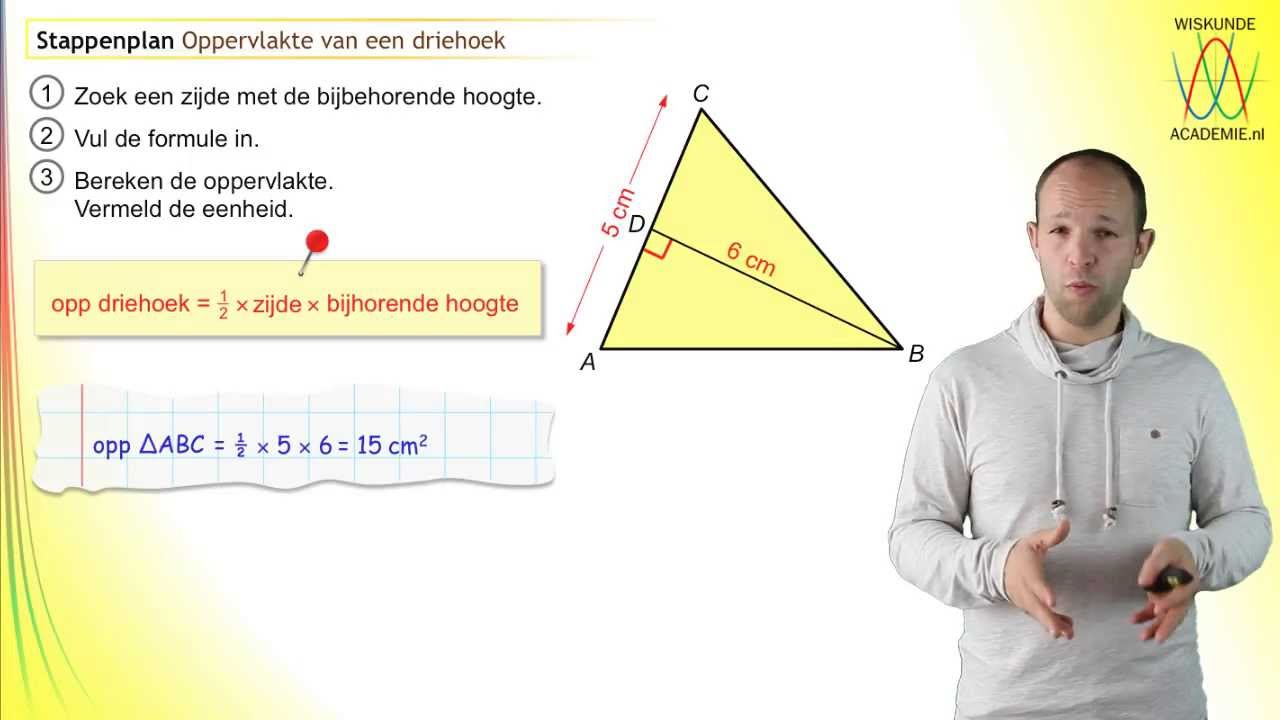
Hoe Bereken Je De Oppervlakte Van Een Driehoek | Taqueria Autentica

Hoe Bereken Je De Oppervlakte Uit In Enkele Eenvoudige Stappen | Taqueria Autentica
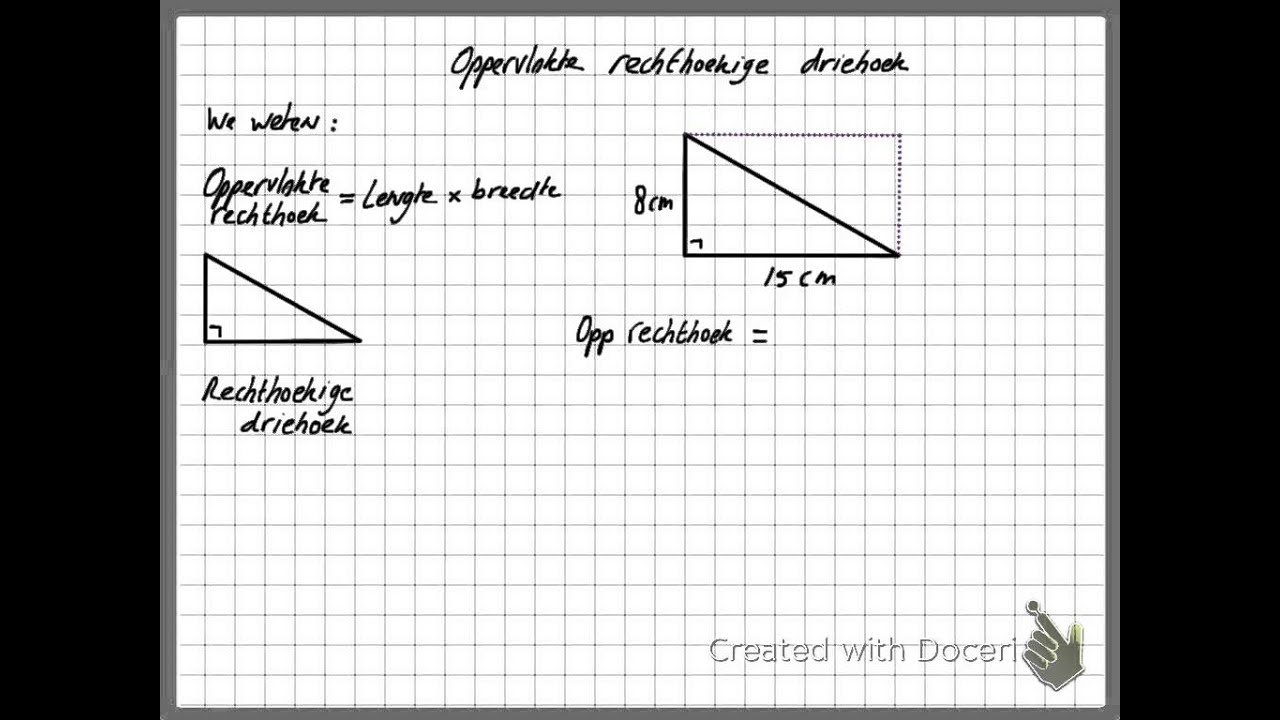
Hoe Bereken Je De Oppervlakte Van Een Rechthoek Een Simpele Gids | Taqueria Autentica