Conquer RLC Circuits: Master the Phasor Diagram
Ever feel like you're wrestling with invisible forces when analyzing AC circuits? RLC circuits, with their resistors, inductors, and capacitors, can be particularly tricky. But fear not! Phasor diagrams are your secret weapon, transforming complex calculations into intuitive visual representations. This guide is your key to unlocking the power of phasor diagrams for RLC circuits.
Imagine trying to juggle voltage and current that constantly shift in time. That's essentially what happens in an AC circuit. Phasor diagrams freeze this action, representing these fluctuating quantities as static vectors. By understanding how to construct and interpret these diagrams, you can easily determine the circuit's overall impedance and phase relationships between voltage and current.
Constructing a phasor diagram for an RLC circuit involves representing the voltage across each component as a rotating vector. The resistor's voltage is in phase with the current, while the inductor's voltage leads the current and the capacitor's voltage lags behind. Combining these vector representations provides a complete picture of the circuit's behavior.
Understanding phasor diagrams dates back to the late 19th century with the development of AC power systems. Charles Proteus Steinmetz, a brilliant mathematician and electrical engineer, popularized their use, significantly simplifying complex AC circuit analysis. These diagrams became indispensable tools for engineers designing and analyzing power systems.
One of the key issues in drawing phasor diagrams is accurately representing the phase differences between voltage and current for each component. Incorrectly representing these phase relationships can lead to inaccurate calculations and a flawed understanding of the circuit’s behavior. This guide will provide clear steps and examples to avoid these pitfalls.
Phasor diagrams reveal critical information about circuit behavior. They simplify impedance calculations, allowing you to visualize the combined effect of resistance, inductance, and capacitance. They clearly illustrate phase relationships, showing how voltage and current align or differ in time. Finally, they help predict circuit response to changes in frequency or component values.
Let's break down creating a phasor diagram for a series RLC circuit: 1) Choose a reference phasor, typically the current. 2) Draw the resistor voltage phasor along the same direction as the current. 3) Draw the inductor voltage phasor 90 degrees ahead (leading) of the current. 4) Draw the capacitor voltage phasor 90 degrees behind (lagging) the current. 5) Vectorially add the individual voltage phasors to find the total voltage across the circuit.
For a parallel RLC circuit, the voltage across each component is the same. Therefore, the voltage phasor becomes the reference. The individual current phasors are then drawn with respect to the voltage, considering the leading and lagging relationships for the inductor and capacitor, respectively.
A practical example: Imagine a series RLC circuit with R=10 ohms, XL=20 ohms (inductive reactance), and XC=15 ohms (capacitive reactance). The net reactance is XL - XC = 5 ohms (inductive). The impedance is calculated using Pythagoras' theorem with R and the net reactance, giving √(10² + 5²) ≈ 11.2 ohms. The phasor diagram shows the voltage leading the current by an angle whose tangent is 5/10.
Challenges can arise when dealing with complex impedances or multiple frequencies. Using phasor algebra or software tools can simplify the process in these scenarios. For instance, software like LTSpice can simulate the circuit and generate accurate phasor diagrams.
FAQs: 1) What is a phasor? (A rotating vector representing a sinusoidal quantity.) 2) Why use phasor diagrams? (Simplify AC circuit analysis.) 3) How are phase differences represented? (By the angle between phasors.) 4) What is impedance? (The opposition to AC current flow.) 5) What is resonance? (When XL=XC.) 6) What is power factor? (Cosine of the phase angle between voltage and current.) 7) How do I determine the leading or lagging nature of the circuit? (By the sign of net reactance.) 8) Where can I learn more about phasors? (Textbooks on circuit analysis, online resources like All About Circuits).
Tip: Always double-check your phase relationships and vector additions to ensure accuracy.
Mastering phasor diagrams is essential for anyone working with AC circuits. They provide a powerful visual tool for understanding complex circuit behavior, enabling you to predict responses to varying frequencies and component values. By understanding the principles and techniques outlined in this guide, you can confidently tackle RLC circuits and unlock a deeper understanding of AC circuit analysis. Start practicing today, and you'll soon find that those once-intimidating circuits become much more manageable. Resources like textbooks, online tutorials, and simulation software can further enhance your understanding and proficiency in using phasor diagrams. Don't just memorize the steps; understand the underlying concepts, and you'll find that phasor diagrams become an invaluable asset in your electrical engineering toolkit.

Circuit Power Factor Calculator | Taqueria Autentica

What is RLC Series Circuit Phasor Diagram Phase Angle | Taqueria Autentica
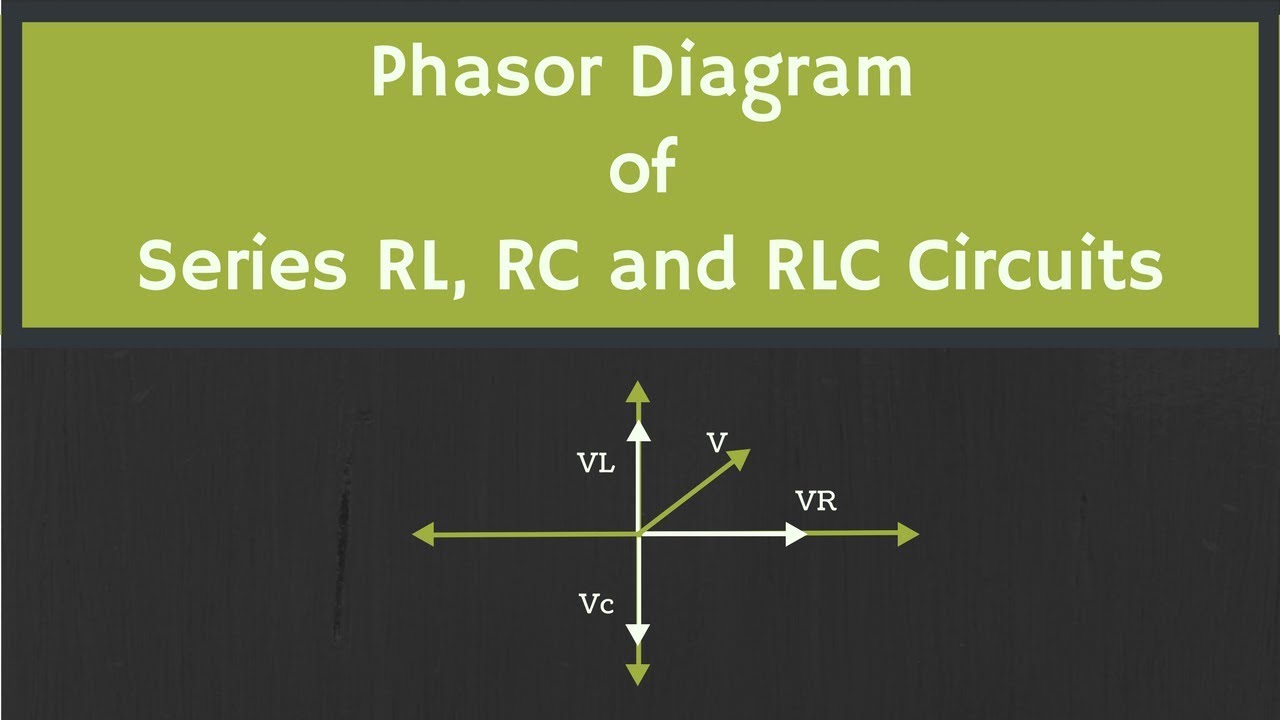
Phasor Diagram Rlc Circuit Series | Taqueria Autentica

Rlc Series Circuit Phasor Diagram | Taqueria Autentica

Phasor Diagram Of Rlc Circuit At Resonance | Taqueria Autentica

Phasor Diagram For RLC Series Circuit | Taqueria Autentica

Series Rlc Circuit Phasor Diagram | Taqueria Autentica

Phasor Diagram Of Rlc Circuit At Resonance | Taqueria Autentica
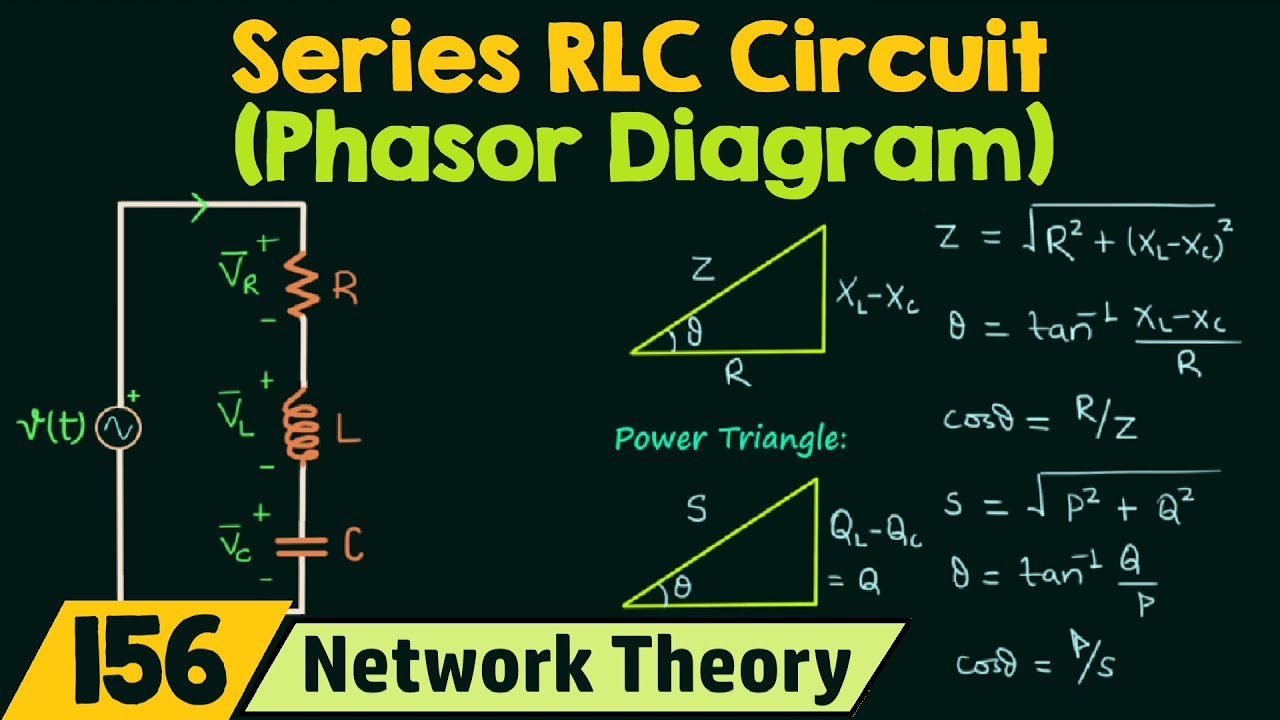
Phasor Diagrams Lcr Circuits | Taqueria Autentica

Series Rlc Circuit Diagram | Taqueria Autentica

Draw Phasor Diagram Rlc Circuit | Taqueria Autentica

Rlc Circuit Phasor Diagram Calculator | Taqueria Autentica

Phasor Diagram Parallel Rc Circuit | Taqueria Autentica

How To Solve Lcr Circuit at Rebbecca Lohman blog | Taqueria Autentica
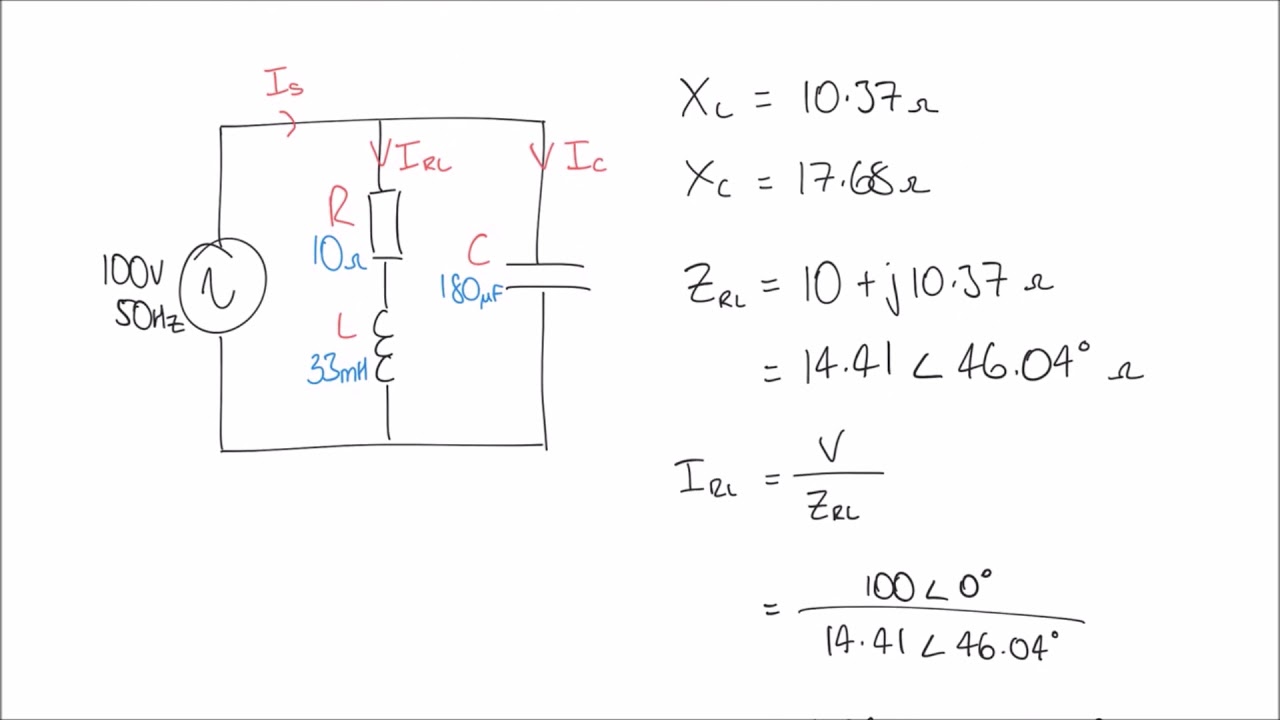
How To Draw Phasor Diagram For Rlc Circuit | Taqueria Autentica