Conquering AC Circuits: Your Phasor Analysis Toolkit
Ever stared at a complex AC circuit and felt a surge of confusion? Those sinusoidal voltages and currents can be a real headache. But fear not, fellow traveler! There’s a powerful tool that can transform these intricate webs of components into something manageable: phasor analysis. This technique allows us to analyze AC circuits in a much simpler way, replacing those oscillating waveforms with static vectors called phasors.
Phasor analysis is like having a secret decoder ring for the world of AC circuits. Instead of wrestling with trigonometric functions and differential equations, we can use the elegance of vector algebra to solve circuit problems. This technique provides a visual and intuitive approach to understanding how voltages and currents relate to each other in AC circuits, particularly when dealing with different frequencies and phase shifts.
Imagine trying to navigate a bustling city without a map. That's what analyzing AC circuits without phasors is like. You're lost in a sea of sine waves. Phasor analysis is your map, your compass, and your guide, helping you navigate the complexities of alternating current circuits with ease and precision.
The foundation of phasor analysis lies in representing sinusoidal functions as rotating vectors, where the length of the vector corresponds to the amplitude of the sine wave, and its angle represents the phase shift. This ingenious method simplifies the process of calculating impedance, voltage drops, and currents in circuits containing resistors, capacitors, and inductors.
By replacing sinusoidal functions with complex numbers, phasor analysis allows us to apply algebraic techniques to solve AC circuit problems, making the analysis much more manageable than using differential equations. Think of it as exchanging a clunky, old-fashioned calculator for a sleek, modern graphing calculator. It's a game-changer!
The history of phasor analysis is closely tied to the development of alternating current systems. Charles Proteus Steinmetz, a brilliant mathematician and electrical engineer, is credited with pioneering the use of complex numbers to represent AC quantities in the late 19th century. This breakthrough simplified the analysis and design of AC power systems, paving the way for the widespread adoption of AC electricity.
Phasor analysis is crucial for understanding and designing AC circuits used in various applications, from power systems to electronics and communication systems. Without phasor analysis, calculating circuit responses to different frequencies and understanding resonance phenomena would be incredibly difficult.
One of the primary challenges in phasor analysis is understanding the concept of phase shift and how it affects the relationship between voltage and current in circuits containing reactive components like capacitors and inductors. A clear understanding of impedance and admittance is also essential for applying phasor techniques effectively.
A simple example of phasor analysis is calculating the impedance of a series RL circuit. By representing the resistance and inductive reactance as phasors, we can use vector addition to find the total impedance. The magnitude of the resulting phasor represents the impedance's magnitude, while its angle represents the phase difference between the voltage and current.
One benefit of phasor analysis is simplifying AC circuit calculations. Instead of using trigonometric identities, we can use simple algebraic operations on complex numbers. Another advantage is its ability to visualize the phase relationships between voltages and currents. Lastly, it allows us to analyze circuits with multiple frequencies, which is essential in communication systems.
Advantages and Disadvantages of Phasor Analysis
| Advantages | Disadvantages |
|---|---|
| Simplifies complex AC circuit calculations | Primarily applicable to sinusoidal steady-state analysis |
| Provides a visual representation of phase relationships | Can be challenging to grasp initially for some learners |
| Enables analysis of circuits with multiple frequencies | Requires a good understanding of complex numbers |
Five Best Practices for Phasor Analysis: 1) Ensure all sources operate at the same frequency; 2) Convert all sinusoidal functions to phasor form; 3) Use impedance and admittance appropriately; 4) Apply Kirchhoff's laws in phasor domain; 5) Convert phasor results back to time-domain waveforms.
Frequently Asked Questions: 1) What is a phasor? 2) How do you convert a sinusoid to a phasor? 3) What is impedance? 4) How do you use phasors to analyze a series RLC circuit? 5) What is resonance in an AC circuit? 6) How does phasor analysis simplify AC calculations? 7) What are the limitations of phasor analysis? 8) What resources can I use to learn more about phasors?
Tips and Tricks: Always double-check your phasor conversions and ensure you're working with the correct units. Visualizing the phasors on a phasor diagram can greatly aid in understanding circuit behavior.
In conclusion, phasor analysis is a powerful tool for unraveling the complexities of AC circuits. By transforming sinusoidal functions into rotating vectors, we can simplify calculations, visualize phase relationships, and analyze circuits with multiple frequencies. Mastering phasor analysis is essential for anyone working with AC circuits, from electrical engineers to electronics technicians. Embrace the power of phasors, and those intimidating AC circuits will become much less daunting. So, grab your metaphorical compass and map, and start exploring the fascinating world of AC circuit analysis with confidence. By understanding the principles and techniques discussed here, you can unlock the secrets of AC circuits and confidently tackle complex circuit problems. Whether you’re a student, a hobbyist, or a professional engineer, phasor analysis is a must-have tool in your electrical toolkit. Start practicing today and see the difference it makes in your understanding of AC circuits.
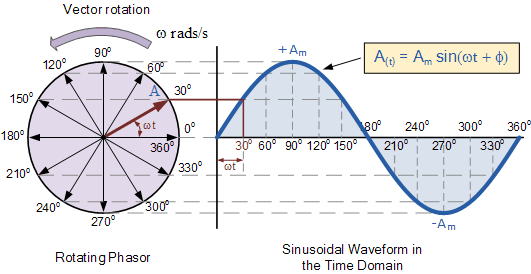
Schneider Electric Phasor Diagram | Taqueria Autentica

Phasor Diagram Of Capacitor | Taqueria Autentica
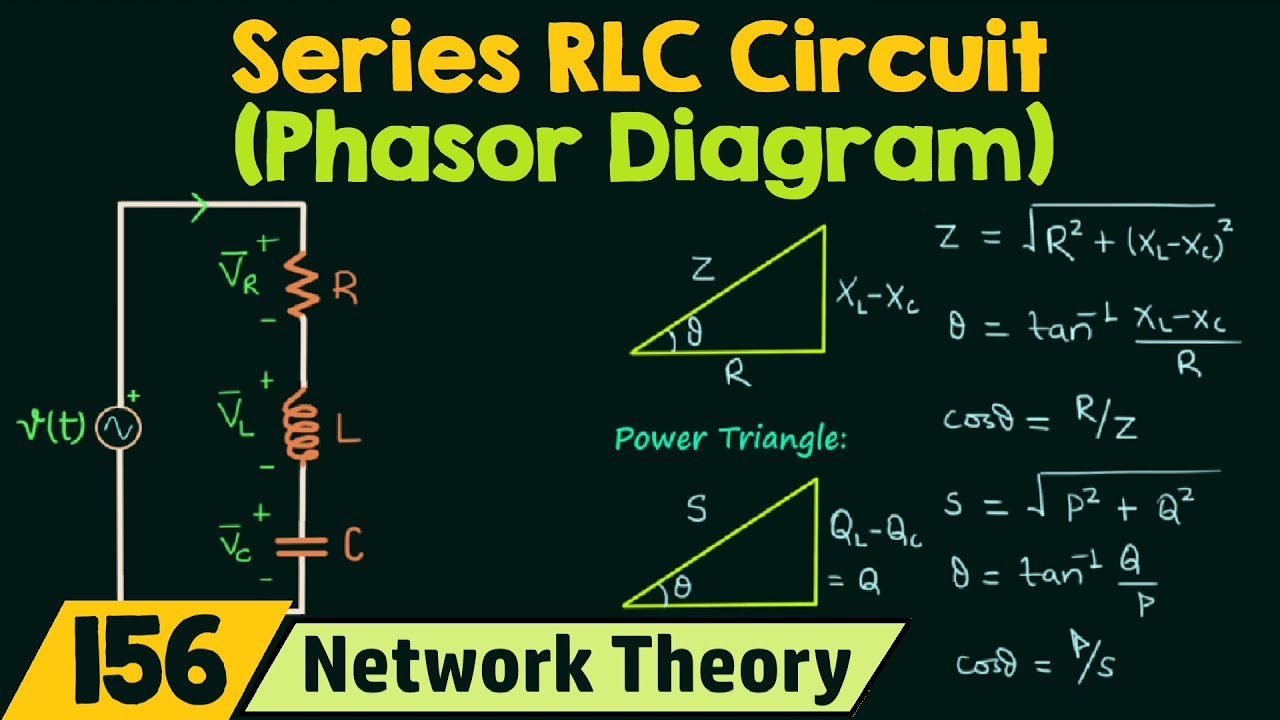
Phasor Diagram Of Ac Circuit | Taqueria Autentica

Basic Phasor Diagram Electric Circuit | Taqueria Autentica

Phasor Representation Of One Phase AC Circuit Presentation | Taqueria Autentica

Meaning Of Purely Resistive at Beverly Eisenbarth blog | Taqueria Autentica

phasor analysis of ac circuit | Taqueria Autentica

Phasor Diagram Rlc Parallel Circuit | Taqueria Autentica

Phase Diagram Of Rl Circuit | Taqueria Autentica
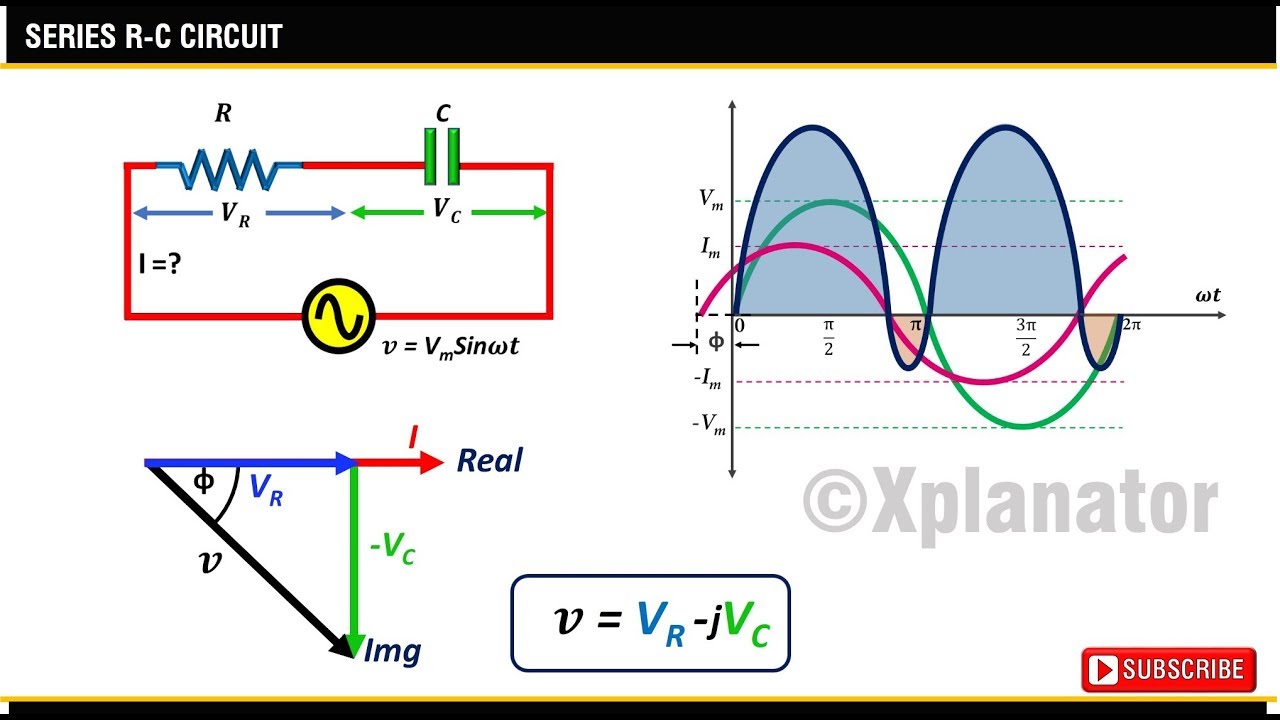
Phasor Diagram For Ac Circuit | Taqueria Autentica

Phasor Diagram Of Rlc Circuit At Resonance | Taqueria Autentica

Simple Steps Nodal and Supernode for AC Circuit | Taqueria Autentica
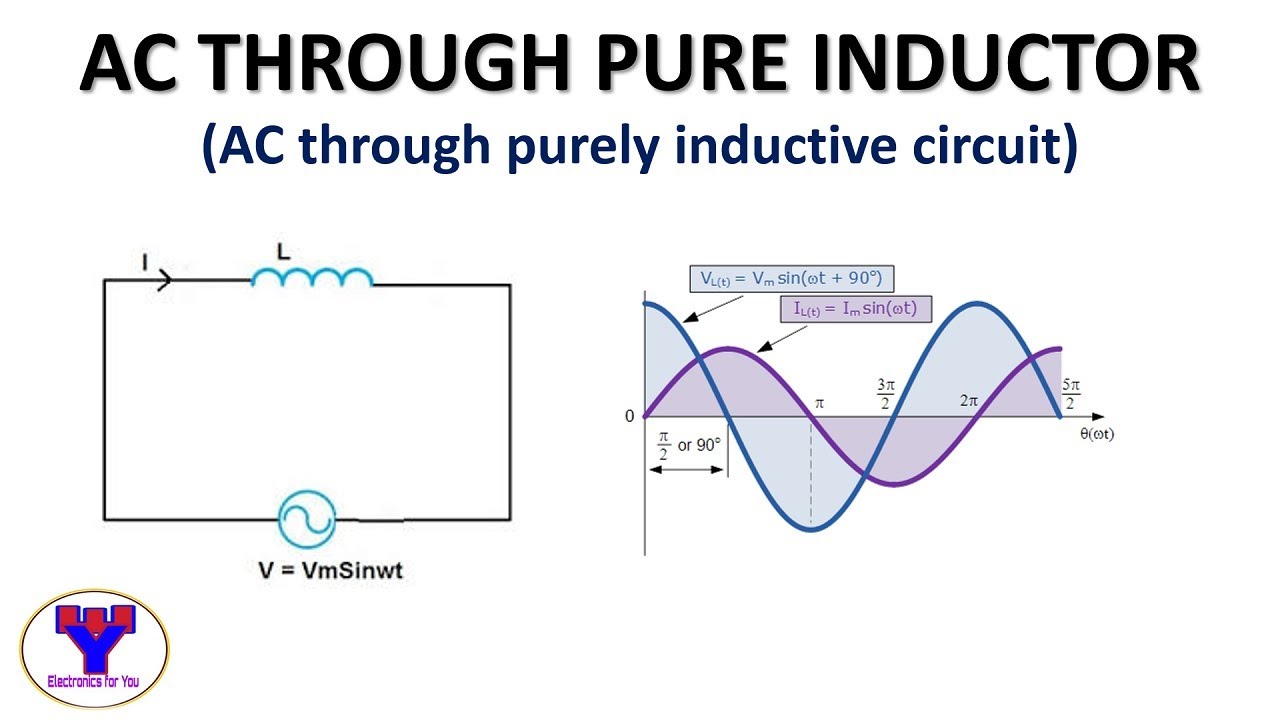
Phasor Diagram For Inductive Circuit | Taqueria Autentica

Phasors Phase Shift and Phasor Algebra | Taqueria Autentica
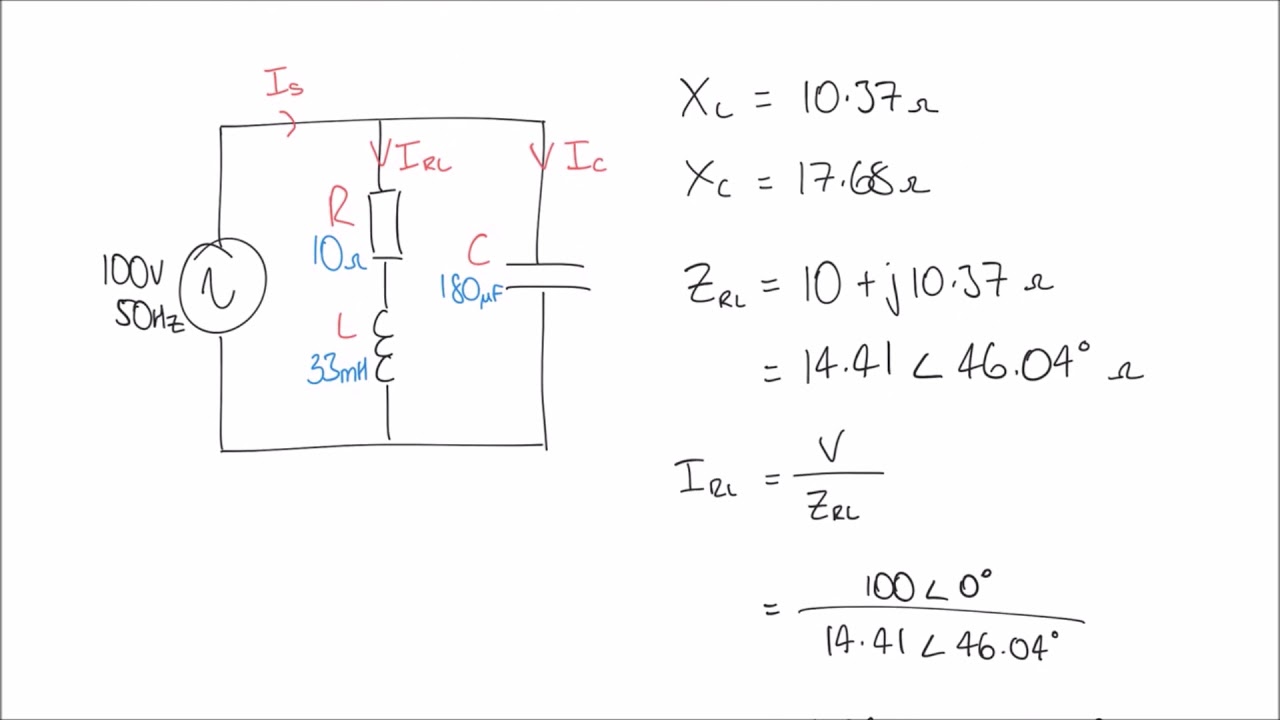
Rlc Circuit Phasor Diagram Calculator | Taqueria Autentica