Mastering Phasor Addition on Your Calculator
Navigating the world of electrical engineering often requires a firm grasp of complex numbers and their representation as phasors. These rotating vectors, essential for analyzing AC circuits, can be tricky to manipulate, especially when adding them together. But what if your calculator could be your ally in this process? This article delves into the efficient use of calculators for phasor addition, unlocking a faster, more accurate approach to circuit analysis.
Imagine effortlessly summing phasors without the cumbersome manual calculations. With a few keystrokes, you can simplify complex circuit problems and gain valuable insights. This article will equip you with the knowledge and techniques to perform phasor addition on your calculator, saving you time and boosting your confidence in tackling intricate electrical engineering challenges. Whether you're a student grappling with circuit theory or a seasoned engineer seeking a more efficient workflow, this guide offers valuable insights into calculator-aided phasor operations.
Phasor addition forms the backbone of AC circuit analysis, playing a critical role in understanding voltage, current, and impedance relationships. Traditionally, phasor addition involved resolving phasors into rectangular components (real and imaginary parts), adding the respective components, and then converting the result back to polar form (magnitude and angle). While this method is foundational, it can be time-consuming and prone to errors. Calculators offer a streamlined alternative, simplifying the process and reducing the risk of mistakes.
The concept of phasors arose from the need to represent sinusoidal quantities in a simplified manner. Charles Proteus Steinmetz, a prominent electrical engineer in the late 19th and early 20th centuries, is credited with popularizing their use. Phasors are essential for analyzing circuits with alternating current and voltage, allowing engineers to represent complex waveforms with a single vector. The ability to add these phasors quickly and accurately is crucial for understanding circuit behavior.
One of the main challenges in performing phasor addition manually is the potential for arithmetic errors during the conversion between rectangular and polar forms. Calculators equipped with complex number functionality address this issue by enabling direct manipulation of phasors in either form. This not only reduces errors but also accelerates the calculation process, allowing for more efficient circuit analysis.
Phasors are represented in two main forms: rectangular (a + jb) and polar (A∠θ). In rectangular form, 'a' represents the real part and 'b' represents the imaginary part. In polar form, 'A' represents the magnitude and 'θ' represents the angle. Most scientific calculators allow you to input and manipulate complex numbers in either form.
For example, consider adding the phasors 3∠30° and 4∠60°. Using a calculator with complex number capabilities, you can enter these phasors directly in polar form and perform the addition. The result will be displayed in either polar or rectangular form, depending on your calculator's settings.
Benefits of calculator-based phasor addition include increased speed, improved accuracy, and streamlined workflow. For instance, calculating the total impedance of a circuit with multiple components can be significantly faster with a calculator, minimizing errors and enabling rapid circuit analysis.
Advantages and Disadvantages of Using a Calculator for Phasor Addition
| Advantages | Disadvantages |
|---|---|
| Speed and Efficiency | Over-Reliance and Loss of Conceptual Understanding (if used without proper foundation) |
| Reduced Errors | Potential Calculator Limitations (some calculators might not handle all complex number operations) |
| Simplified Workflow | Battery Dependence |
Best Practices:
1. Understand the underlying principles of phasor addition before relying solely on a calculator.
2. Verify your calculator's complex number capabilities and familiarize yourself with its functions.
3. Double-check your inputs to avoid errors.
4. Interpret the results in the correct context of the circuit problem.
5. Consider using a calculator with built-in functions for converting between rectangular and polar forms.
FAQs:
1. Q: Can all calculators perform phasor addition? A: Most scientific and engineering calculators have complex number functionalities.
2. Q: What is the difference between rectangular and polar form? A: Rectangular form represents a phasor using its real and imaginary components, while polar form uses magnitude and angle.
3. Q: How do I enter a phasor in polar form on my calculator? A: Consult your calculator's manual for specific instructions, as it varies between models. Generally, it involves entering the magnitude, angle, and using a specific function key.
4. Q: How do I convert between rectangular and polar form on my calculator? A: Most calculators have built-in functions for this conversion (often labeled as "Rect" to "Polar" or "Polar" to "Rect").
5. Q: What are some common mistakes to avoid when adding phasors on a calculator? A: Ensure correct angle mode (degrees or radians), proper input format, and understanding the meaning of the results.
6. Q: Are there any online resources for learning more about phasor addition? A: Yes, numerous websites and online tutorials cover this topic in detail.
7. Q: Can I use a graphing calculator for phasor addition? A: Yes, graphing calculators are well-suited for complex number operations, including phasor addition.
8. Q: How important is understanding phasors in electrical engineering? A: Phasors are fundamental to AC circuit analysis and are crucial for understanding many electrical concepts.
In conclusion, mastering phasor addition on a calculator is an invaluable skill for any electrical engineer. By leveraging the power of these tools, you can streamline complex calculations, reduce errors, and gain deeper insights into circuit behavior. While calculators offer a convenient and efficient approach, it's crucial to develop a strong understanding of the underlying principles of phasor arithmetic. This combined approach of theoretical knowledge and practical tool utilization will empower you to confidently tackle the most challenging circuit analysis problems. Start practicing today and experience the transformative benefits of calculator-aided phasor addition in your electrical engineering journey.

how to add phasors on calculator | Taqueria Autentica

R22190k Salary After Tax in South Africa | Taqueria Autentica

how to add phasors on calculator | Taqueria Autentica

Obtención de expresión sinusoidal | Taqueria Autentica

how to add phasors on calculator | Taqueria Autentica

Fraction to Decimal Calculator | Taqueria Autentica

Complex Numbers Phasors in Polar and Rectangular Form | Taqueria Autentica

hi can someone explain to me how to add phasors to | Taqueria Autentica
Hi Regan thanks for reaching out Sure id love to have the article | Taqueria Autentica

how to add phasors on calculator | Taqueria Autentica
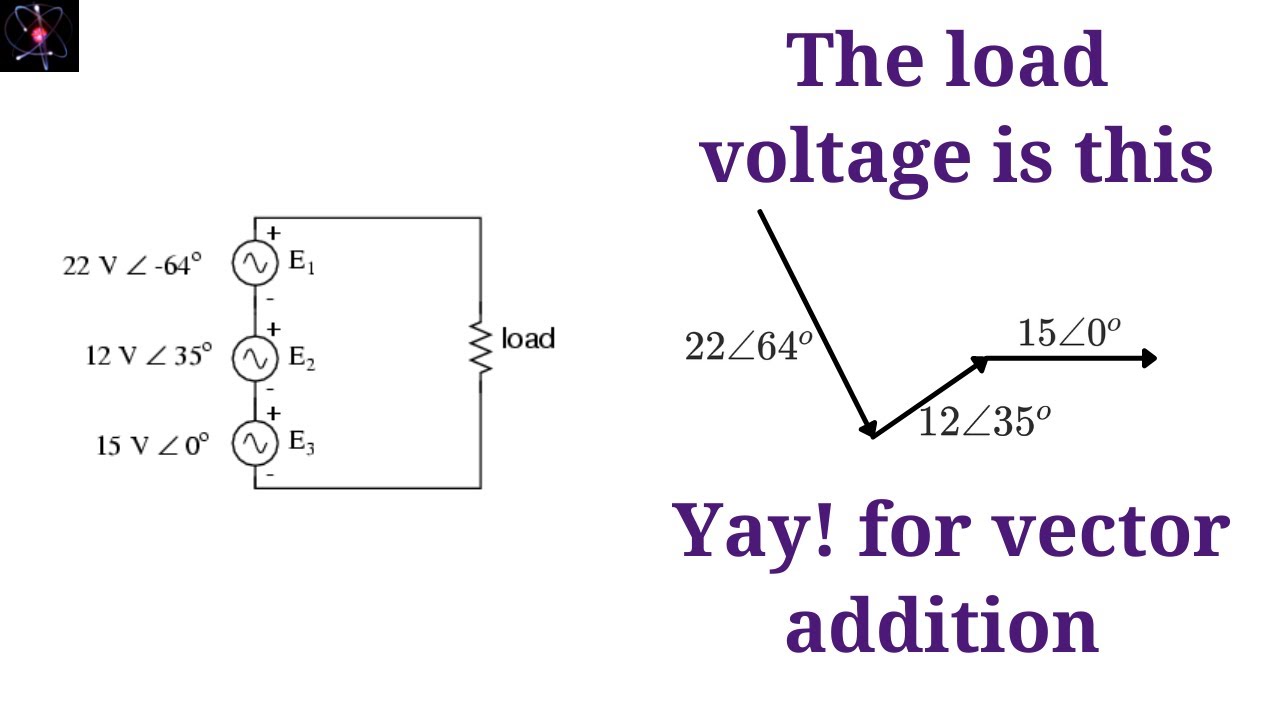
AC Chapter 2 Complex Numbers | Taqueria Autentica

Rectangular to Polar form Polar to Rectangular form conversion | Taqueria Autentica

how to add phasors on calculator | Taqueria Autentica

R4724399k Salary After Tax in South Africa | Taqueria Autentica

Complex Numbers Phasors in Polar and Rectangular Form | Taqueria Autentica