Midsegment Of A Triangle Formula

11 Jan 2024

Have you ever wondered about the midsegment of a triangle formula and its significance in geometry? Well, look no further as we delve into this interesting topic and explore its history, definition, benefits, challenges, and practical applications. Join me on this journey of discovery as we unravel the secrets of the midsegment of a triangle formula.

History, Origin, Importance of Midsegment of a Triangle Formula

The midsegment of a triangle formula has been a fundamental concept in geometry for centuries. It plays a crucial role in understanding the properties of triangles and their various components. Without the midsegment formula, our understanding of triangles and their relationships would be incomplete. This formula has paved the way for many important theorems and principles in geometry, making it an indispensable tool for mathematicians and students alike.

Definition, Explanation, and Simple Examples of Midsegment of a Triangle Formula

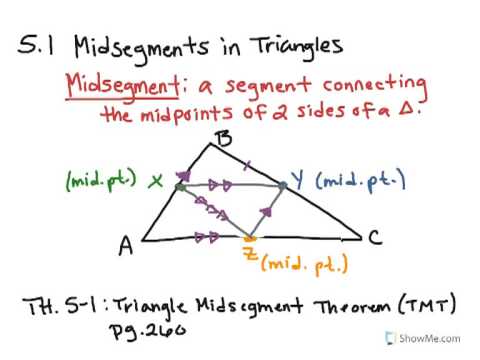
The midsegment of a triangle is a line segment that connects the midpoints of two sides of a triangle. It is parallel to the third side of the triangle and half its length. The formula for calculating the length of the midsegment involves basic principles of geometry and algebra. For example, in a triangle ABC with midpoints D and E on sides AB and AC respectively, the midsegment DE is parallel to BC and half its length.

Benefits of Midsegment of a Triangle Formula

Simplifies Triangle Analysis: The midsegment formula provides a straightforward method for analyzing the properties of triangles without complex calculations.
Helps in Construction: Architects and engineers use the midsegment formula to ensure the accuracy and stability of triangular structures.
Aids in Proofs: The midsegment of a triangle is often used as a critical step in proving various geometric theorems and properties.

Action Plan for Implementing Midsegment of a Triangle Formula

To effectively utilize the midsegment of a triangle formula, one must first identify the midpoints of the sides and understand the concept of parallel lines. By following a systematic approach and practicing with different triangle configurations, one can master the application of the midsegment formula in various geometric problems.

Checklist for Midsegment of a Triangle Formula

Identify the midpoints of the sides of the triangle.
Verify the parallel relationships between the midsegment and the third side.
Calculate the length of the midsegment using the appropriate formula.

Step-by-Step Guide on Midsegment of a Triangle Formula

Locate the midpoints of the sides of the triangle.
Determine the midpoint of the third side if needed.
Calculate the length of the midsegment based on the given information.

Recommendations for Learning Midsegment of a Triangle Formula

For further exploration of the midsegment of a triangle formula, I recommend checking out online resources such as Khan Academy, Mathway, and Geometry Dash. These platforms offer interactive lessons, practice problems, and visual demonstrations to enhance your understanding of this topic.

Advantages and Disadvantages of Midsegment of a Triangle Formula

Advantages:

Simplifies triangle analysis.
Facilitates geometric proofs.
Helps in construction projects.

Disadvantages:

May require advanced algebraic skills.
Limited application in non-triangular geometry.
Complexity increases with more complex triangle configurations.

Best Practices for Implementing Midsegment of a Triangle Formula

Always double-check the midpoint calculations for accuracy.
Ensure a clear understanding of parallel lines and transversals.
Practice with a variety of triangle scenarios to strengthen your problem-solving skills.

Real-Life Examples of Midsegment of a Triangle Formula

In bridge construction, engineers use the midsegment formula to ensure the stability of triangular trusses.
Architects apply the midsegment concept to design triangular structures with precise measurements.
Surveyors use the midsegment formula for accurate land mapping and boundary surveys.

Challenges and Solutions for Midsegment of a Triangle Formula

Challenges:

Identifying midpoints accurately.
Applying the formula to irregular triangles.
Understanding the implications of parallel lines in geometry.

Solutions:

Use geometry tools for precise midpoint calculations.
Break down complex triangles into simpler components.
Practice with different triangle configurations to enhance your skills.

Common Questions about Midsegment of a Triangle Formula

What is the midsegment of a triangle?
- The midsegment is a line segment connecting the midpoints of two sides of a triangle.
Why is the midsegment important in geometry?
- It helps in analyzing triangle properties and proving geometric theorems.
How do I calculate the length of the midsegment?
- Use the midpoint formula and the concept of parallel lines to determine the midsegment length.

Tips and Tricks for Mastering Midsegment of a Triangle Formula

Draw accurate diagrams to visualize triangle components.
Practice with different triangle types to enhance your problem-solving skills.
Break down complex problems into smaller steps for better understanding.

Conclusion: Unveiling the Secrets of Midsegment of a Triangle Formula

In conclusion, the midsegment of a triangle formula is a powerful tool that enhances our understanding of geometric relationships and shapes. By mastering this formula, we can unlock a world of possibilities in geometry, construction, and engineering. So, embrace the challenge, explore the benefits, and take your geometric skills to new heights with the midsegment of a triangle formula. Start practicing today and unleash your potential in the realm of geometry!