Unlocking Circuit Secrets: Mastering Phasor Analysis
Ever wondered how electrical engineers analyze complex alternating current (AC) circuits? The secret lies in a powerful tool called phasor analysis. This technique simplifies circuit calculations by representing sinusoidal voltages and currents as rotating vectors, known as phasors. Understanding how to calculate the phasor representation of current (often denoted as 'I') is fundamental to this process. Let's unravel the mysteries of phasor 'I' and its significance in electrical engineering.
Imagine trying to analyze a circuit with multiple AC sources operating at different frequencies. The traditional time-domain analysis becomes incredibly complex. Phasors come to the rescue by transforming these time-varying signals into static vectors in the frequency domain, making calculations significantly easier. Determining the phasor 'I' is crucial for understanding current flow, impedance calculations, and overall circuit behavior.
The concept of phasors arose from the need to simplify AC circuit analysis. Charles Proteus Steinmetz, a renowned electrical engineer, pioneered the use of phasor diagrams in the late 19th century. This graphical representation of sinusoidal quantities revolutionized the field, enabling engineers to tackle complex circuits with relative ease. Today, determining the phasor representation of current remains a cornerstone of electrical engineering education and practice.
The importance of determining phasor I lies in its ability to simplify complex AC circuit calculations. It allows engineers to analyze circuits with multiple sources and various components, such as resistors, capacitors, and inductors, without resorting to cumbersome differential equations. This streamlined approach is essential for designing and analyzing power systems, communication networks, and electronic circuits.
One of the main issues related to phasor analysis is ensuring a clear understanding of the underlying concepts. Students and practitioners must grasp the relationship between the time-domain representation of a sinusoidal signal and its corresponding phasor in the frequency domain. A strong foundation in complex numbers is also essential for performing phasor calculations accurately.
A phasor is a complex number representing the amplitude and phase of a sinusoidal quantity. For example, if the current in a circuit is i(t) = Im*cos(ωt + θ), where Im is the peak amplitude, ω is the angular frequency, and θ is the phase angle, the corresponding phasor I is given by I = Im*e^(jθ), where j is the imaginary unit. This complex representation captures both the magnitude and phase information of the current.
Calculating phasor I typically involves converting the time-domain representation of the current into its phasor equivalent using the complex exponential form. This conversion process often involves applying trigonometric identities and complex number algebra. For instance, if the current is expressed as a sine function, it needs to be converted to its cosine equivalent before determining the phasor.
Benefits of using phasor analysis:
1. Simplified Calculations: Phasors transform differential equations into algebraic equations, making circuit analysis much easier.
2. Visualization: Phasor diagrams provide a visual representation of the relationship between voltage and current in a circuit.
3. Frequency Domain Analysis: Phasors facilitate analysis in the frequency domain, which is essential for understanding circuit behavior at different frequencies.
Frequently Asked Questions about Phasor I:
1. What is a phasor? - A phasor is a complex number representing the amplitude and phase of a sinusoidal quantity.
2. Why are phasors used? - They simplify AC circuit analysis by transforming time-varying signals into static vectors.
3. How is phasor I calculated? - It is determined by converting the time-domain representation of current into its complex exponential form.
4. What is the significance of phasor I? - It is essential for understanding current flow, impedance, and circuit behavior.
5. What are the challenges in understanding phasors? - A solid grasp of complex numbers and the relationship between time and frequency domains is crucial.
6. How are phasors related to impedance? - Impedance is represented as a complex number in phasor analysis, relating voltage and current phasors.
7. What software can be used for phasor analysis? - Circuit simulation software like LTspice or PSpice can perform phasor calculations.
8. Where can I learn more about phasors? - Textbooks on circuit analysis and online resources provide in-depth information.
In conclusion, determining the phasor I is fundamental to AC circuit analysis. It simplifies calculations, enables visualization of circuit behavior, and facilitates frequency domain analysis. Mastering this technique is essential for electrical engineers and anyone working with AC circuits. By understanding the concepts, applying appropriate calculations, and utilizing available resources, you can unlock the power of phasor analysis and gain a deeper understanding of circuit behavior. So, dive into the world of phasors and discover the secrets they hold for unlocking the complexities of AC circuits. Start exploring and empower yourself with the knowledge to analyze and design efficient and robust electrical systems.

Phasor Representation Of One Phase AC Circuit Presentation | Taqueria Autentica
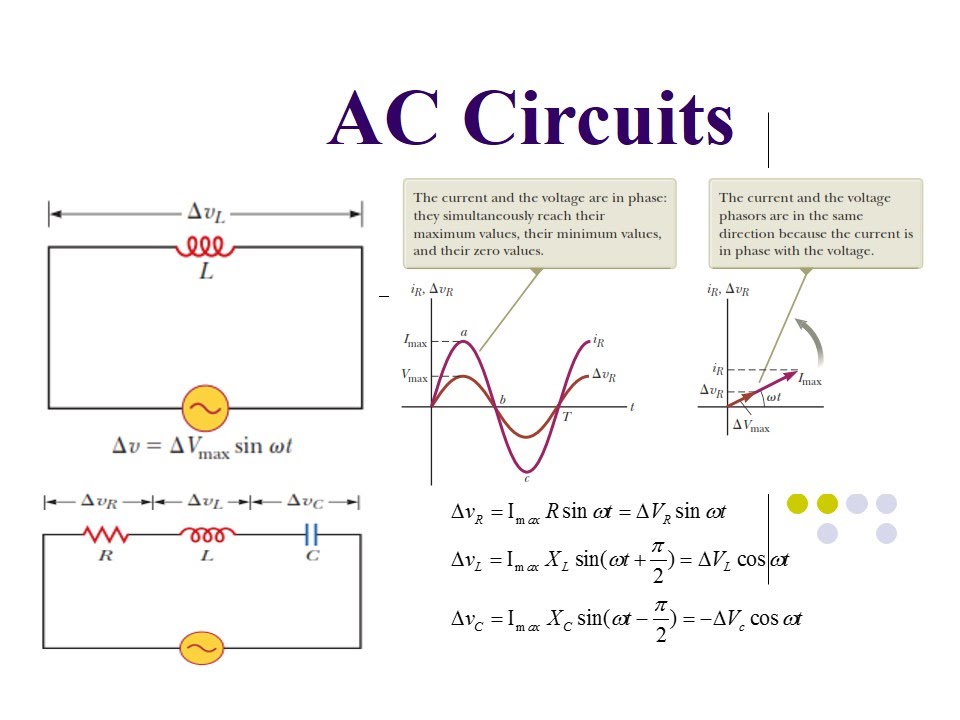
Rc Series Circuit With Ac Source | Taqueria Autentica

Phasor Diagram Of Ac Circuit | Taqueria Autentica
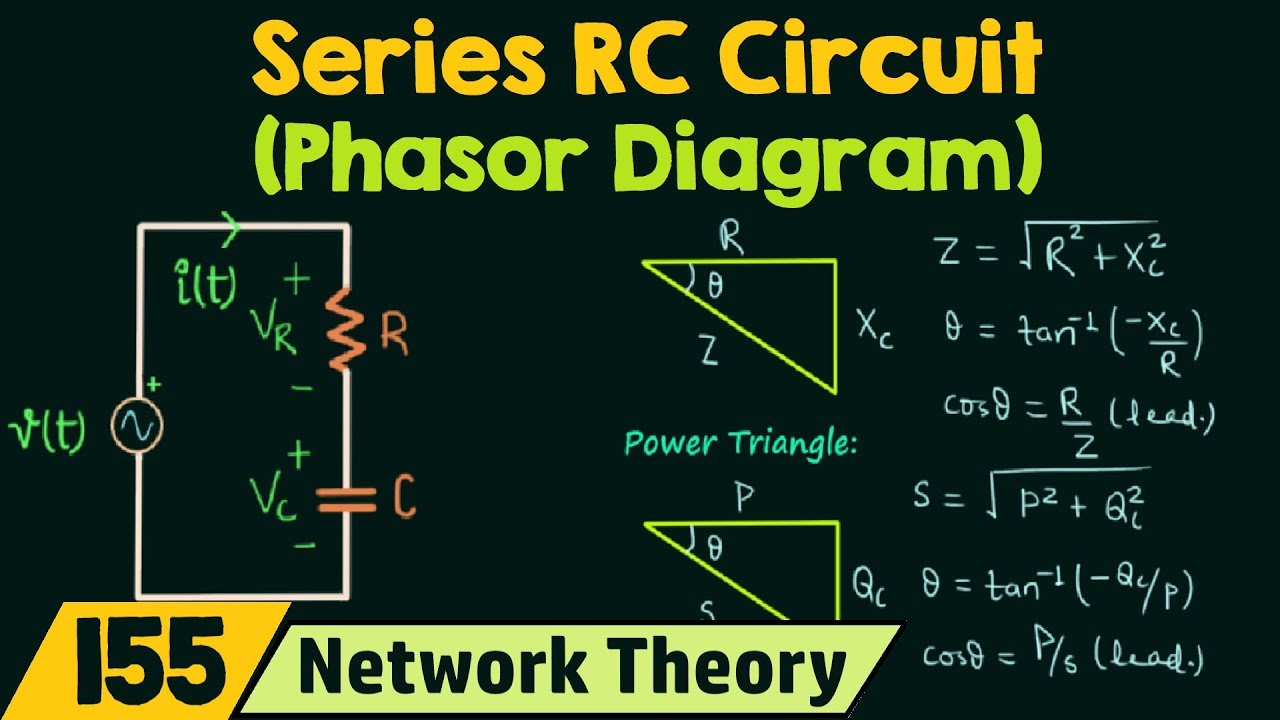
Phasor Diagram Of Rc Series Circuit | Taqueria Autentica

Phasor Diagrams Of Ac Circuits | Taqueria Autentica
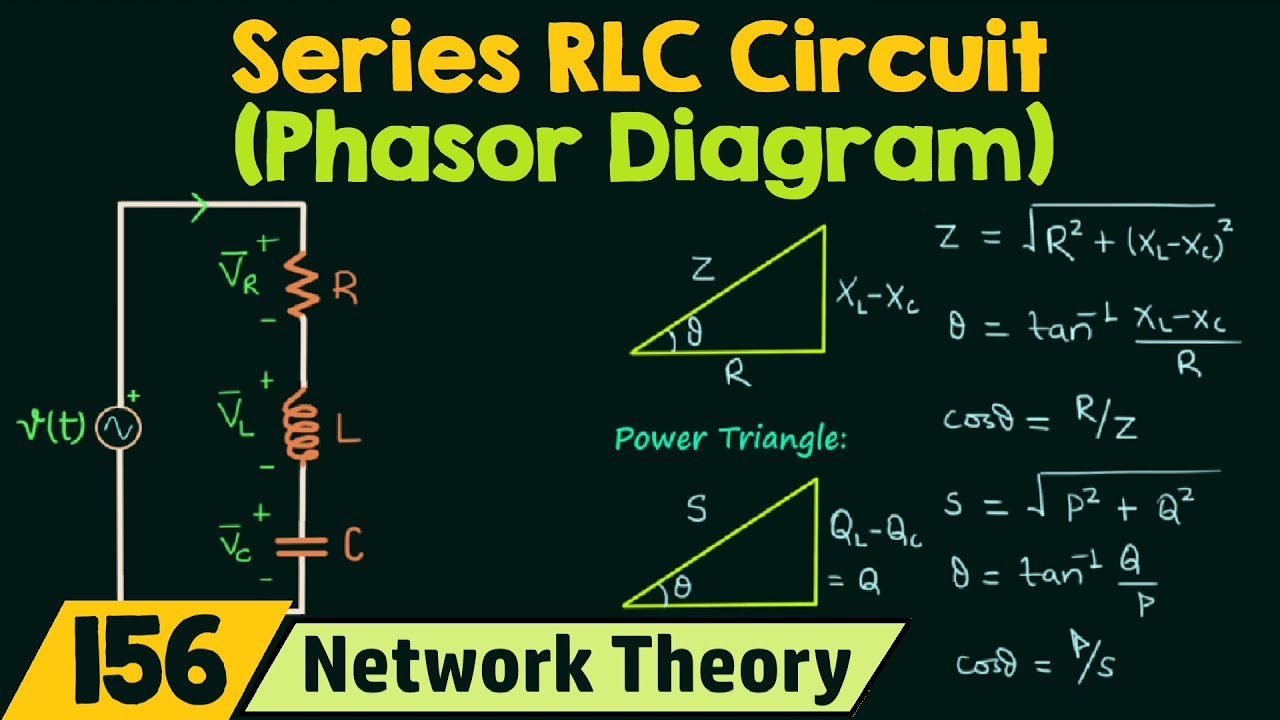
12 Phasor Diagram Of Rlc Series Circuit | Taqueria Autentica

How To Draw Phasor Diagram at How To Draw | Taqueria Autentica
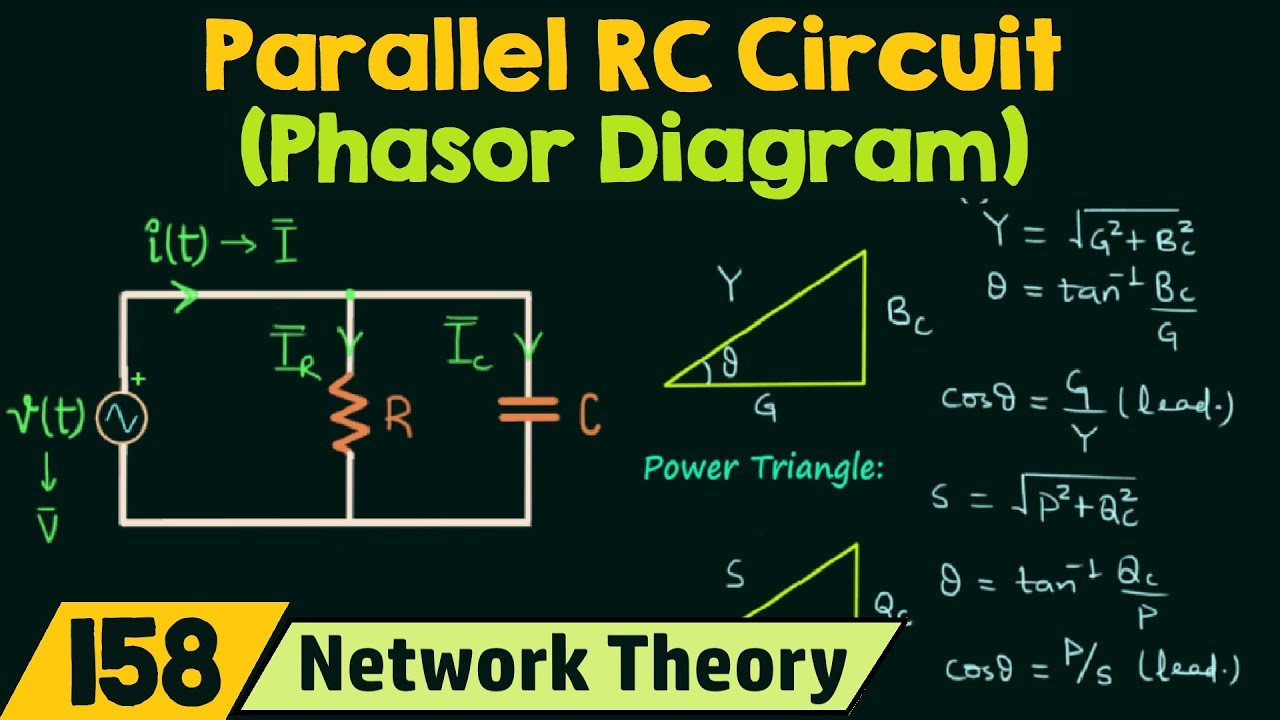
find the phasor i | Taqueria Autentica
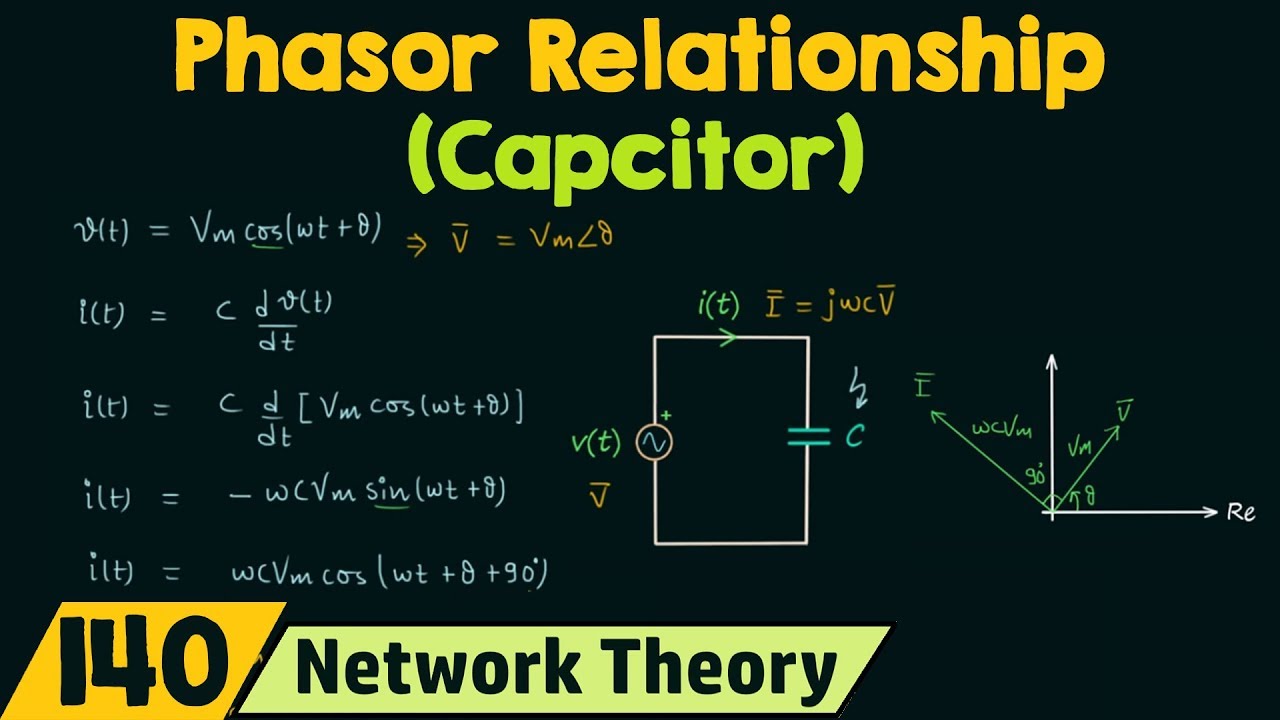
Phasor Diagram Of Capacitor | Taqueria Autentica

Basic Phasor Diagram Electric Circuit | Taqueria Autentica

Phasor Diagrams For Ac Circuits | Taqueria Autentica

Converter Circuit Phasor Diagram | Taqueria Autentica