Unlocking Circuit Secrets: Understanding Phasors
Ever wondered how electrical engineers tackle the complexities of alternating current (AC) circuits? The secret lies in a powerful tool called a phasor. This article will unravel the mystery of what a phasor is in circuits and demonstrate its significance in simplifying AC circuit analysis.
Imagine trying to analyze a circuit where voltages and currents are constantly changing. It quickly becomes a mathematical nightmare. Phasors offer an elegant solution by representing these sinusoidal quantities as static vectors, making calculations significantly easier. Instead of grappling with time-varying functions, we can use simple vector algebra to analyze complex AC circuits.
Phasor representation provides a visual and intuitive understanding of the relationships between voltage and current in AC circuits. By representing these quantities as vectors rotating in the complex plane, we can easily visualize phase differences and calculate impedance, power, and other important circuit parameters. This graphical approach is far more manageable than working with trigonometric functions directly.
The concept of a phasor is deeply rooted in complex number theory. A phasor is essentially a complex number that represents the amplitude and phase of a sinusoidal function. The magnitude of the phasor corresponds to the amplitude of the sinusoid, while the angle of the phasor represents the phase shift. This concise representation simplifies calculations involving sinusoidal signals.
Understanding phasors is fundamental to electrical engineering, particularly in areas like power systems analysis, communication systems, and control systems. They are essential for analyzing and designing circuits involving inductors, capacitors, and resistors subjected to AC signals. Without phasors, analyzing these circuits would be incredibly complex and time-consuming.
Historically, Charles Proteus Steinmetz is credited with popularizing the use of phasors in AC circuit analysis. His work in the late 19th and early 20th centuries revolutionized the way engineers approach complex electrical systems. The main issue phasors address is the difficulty of handling sinusoidal quantities mathematically. Phasors transform these dynamic values into static vectors, simplifying calculations significantly.
A phasor is a complex number representing a sinusoidal function whose amplitude (A), angular frequency (ω), and initial phase (θ) are time-invariant. It simplifies the analysis of AC circuits by transforming differential equations into algebraic equations.
A simple example: Consider a voltage source v(t) = Vm*cos(ωt + θ). Its phasor representation is V = Vm∠θ, where Vm is the magnitude and θ is the phase angle. This simplifies calculations involving this voltage source in a circuit.
Benefits of using phasors include simplified calculations, clearer visualization of circuit behavior, and easier analysis of complex circuits.
An action plan for implementing phasor analysis involves identifying the sinusoidal quantities in the circuit, converting them to their phasor equivalents, performing calculations using complex algebra, and then converting the results back to the time domain.
Recommendations: "Engineering Circuit Analysis" by Hayt and Kemmerly is a great resource for learning more about phasors and AC circuit analysis.
Advantages and Disadvantages of Using Phasors
| Advantages | Disadvantages |
|---|---|
| Simplifies AC circuit analysis | Applicable only to sinusoidal steady-state conditions |
| Facilitates visualization of circuit behavior | Requires understanding of complex numbers |
| Enables easier calculation of impedance and power |
Best Practices: 1. Ensure all sinusoidal functions have the same frequency. 2. Clearly define the reference phasor. 3. Double-check conversions between time domain and phasor domain. 4. Use appropriate software tools for complex number calculations. 5. Verify results using alternative methods when possible.
Example 1: Analyzing a series RLC circuit using phasors to calculate impedance and current.
Example 2: Determining the voltage across a capacitor in a parallel RC circuit.
Example 3: Calculating power factor in an AC circuit using phasor analysis.
Example 4: Analyzing a three-phase AC circuit using phasor diagrams.
Example 5: Designing a filter circuit using phasor concepts.
Challenge 1: Dealing with non-sinusoidal waveforms. Solution: Use Fourier analysis to decompose the waveform into sinusoidal components.
FAQ 1: What is the difference between a phasor and a vector? Answer: A phasor is a complex representation of a sinusoidal function, while a vector is a more general mathematical entity.
Tips and Tricks: When working with phasors, always remember to convert back to the time domain for the final answer. Use graphical tools like phasor diagrams to visualize circuit behavior.
In conclusion, understanding what a phasor is in circuits is crucial for anyone working with AC systems. Phasors simplify complex calculations, enable visualization of circuit behavior, and provide a powerful tool for analyzing and designing a wide range of electrical circuits. From power systems to communication networks, phasors play a vital role in shaping our modern world. By mastering the concept of phasors, engineers can unlock the secrets of AC circuits and pave the way for innovative technological advancements. Embracing phasor analysis opens doors to understanding complex electrical phenomena, allowing for more efficient and effective circuit design and analysis. Take the time to explore the resources mentioned and delve deeper into this fascinating aspect of electrical engineering.
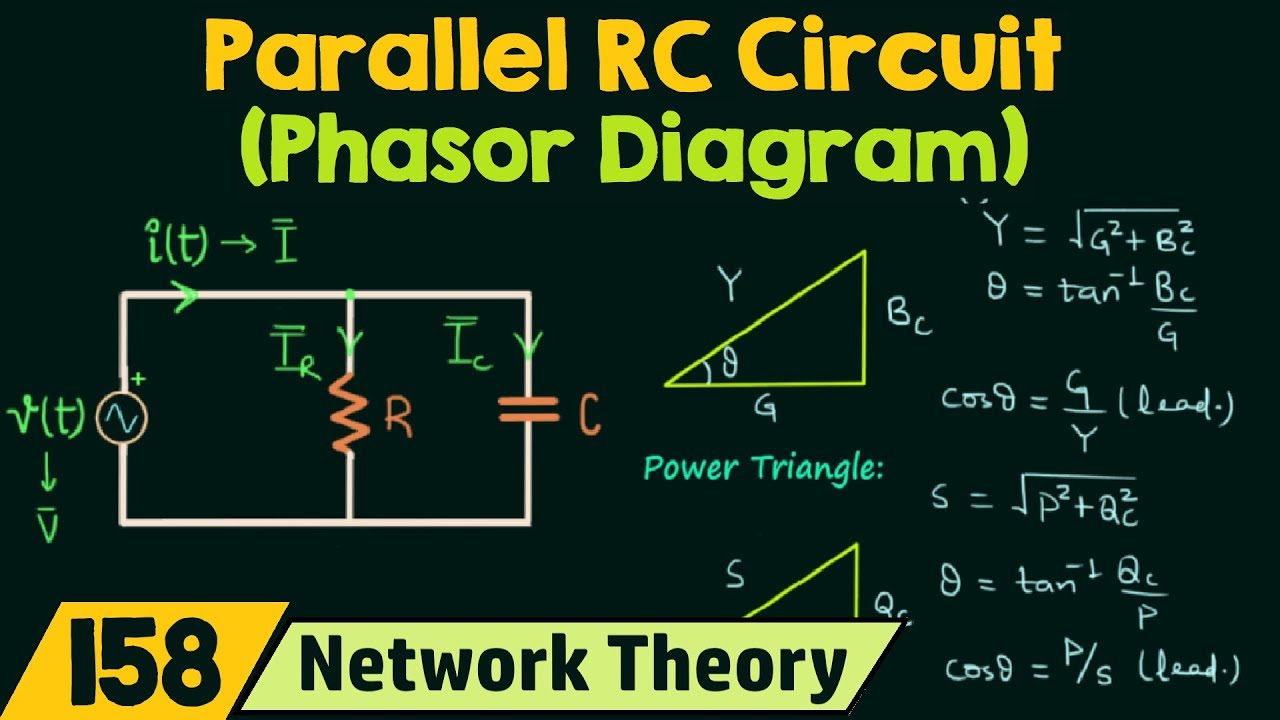
Phasor Diagrams In Rc Circuit | Taqueria Autentica

Phasor Diagram Of Rl Circuit | Taqueria Autentica

Phasor Diagram Inductive Circuit | Taqueria Autentica

Phasor Diagrams Lcr Circuits | Taqueria Autentica
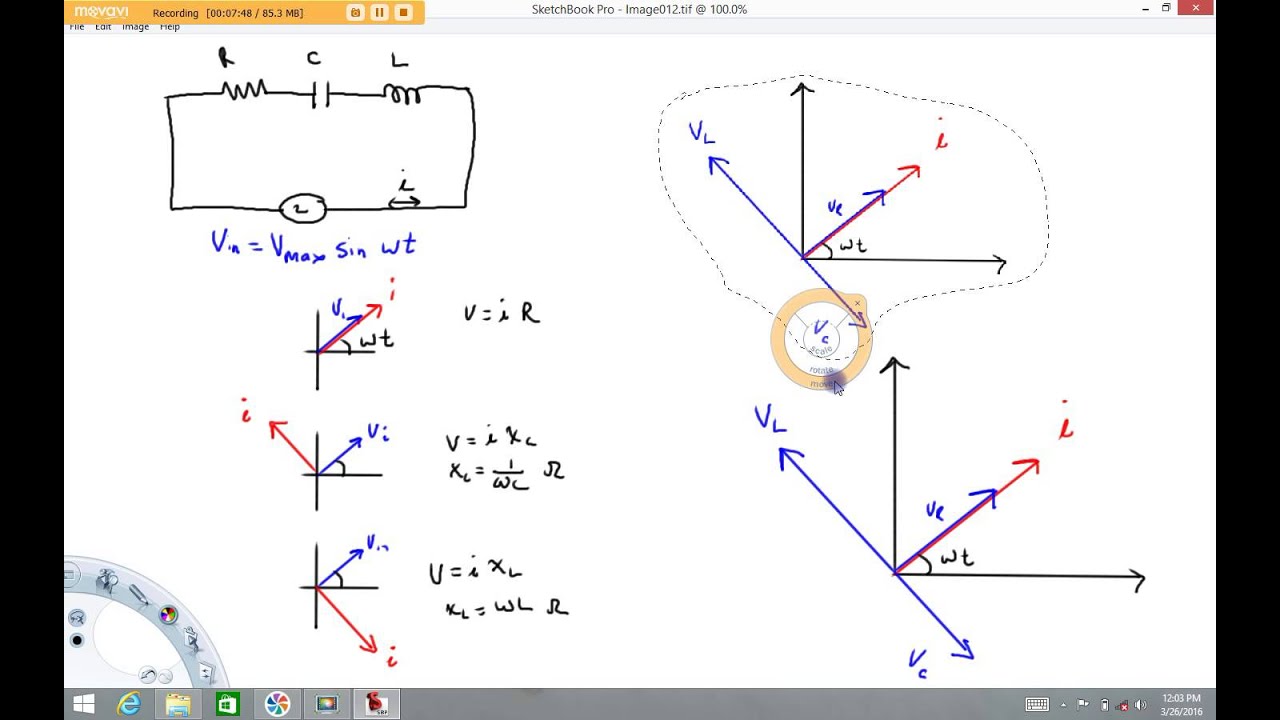
Phasor Diagram For Rc Circuit | Taqueria Autentica
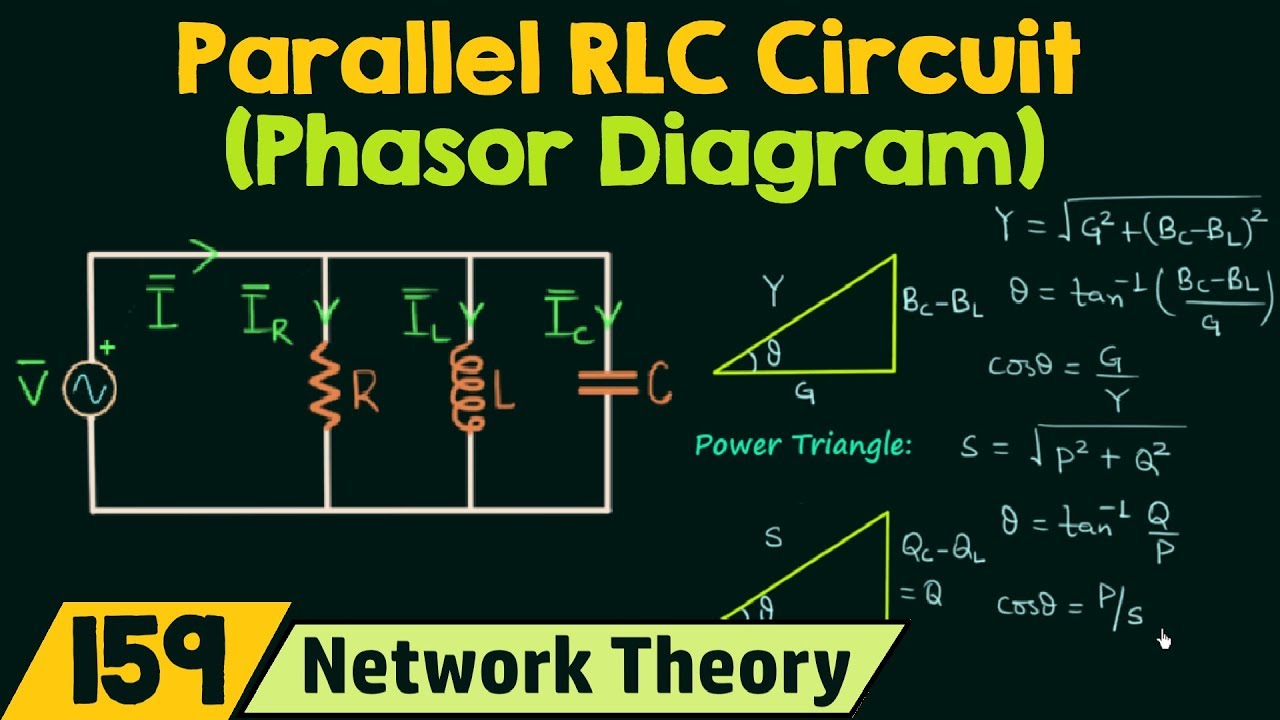
Phasor Diagram Rlc Circuit Resonance | Taqueria Autentica
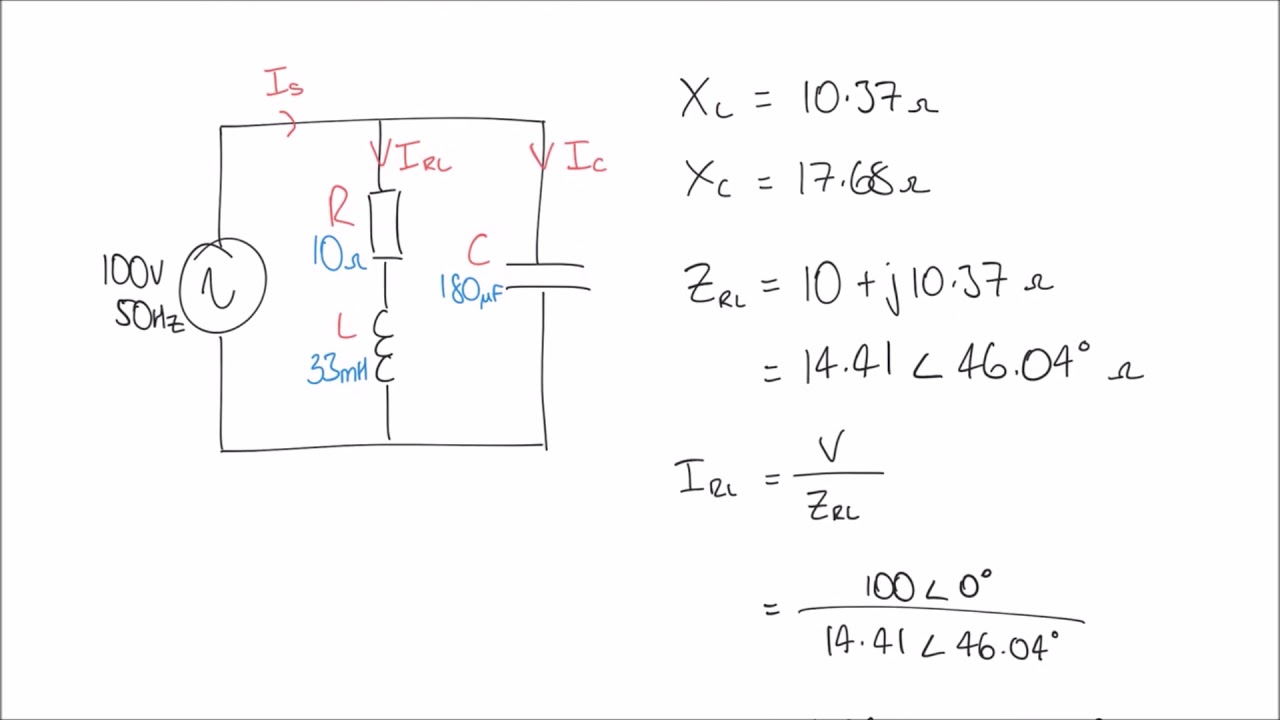
Rlc Circuit Phasor Diagram Calculator | Taqueria Autentica

DIAGRAM 4 Wire 3 Phase Vector Diagram | Taqueria Autentica
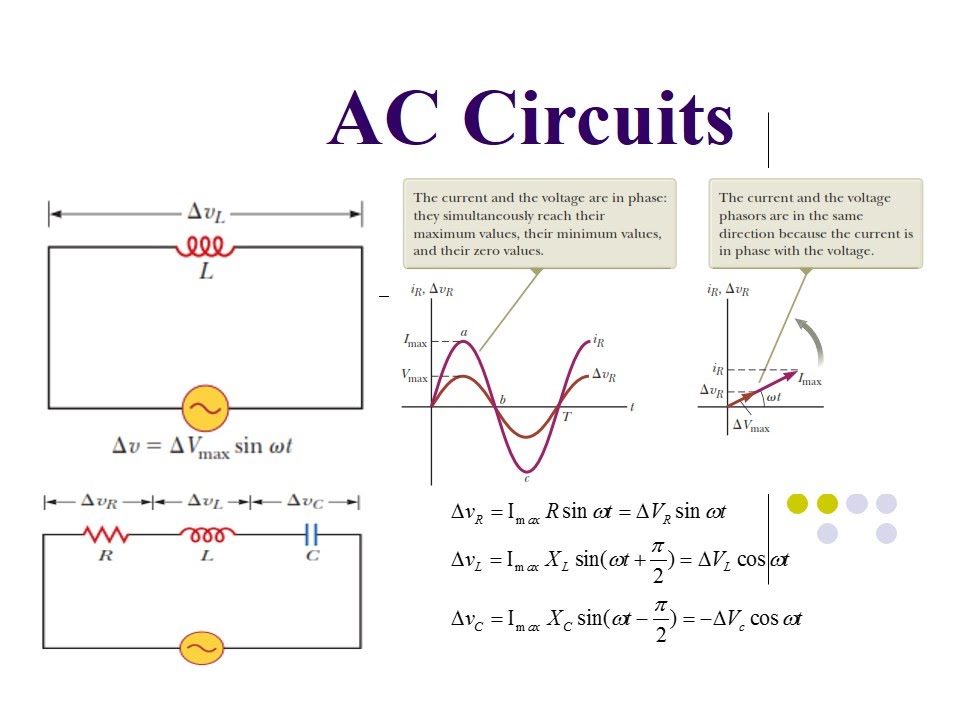
Ac Circuit Phasor Diagram Impedance | Taqueria Autentica

Phasor Diagram For Ac Circuit | Taqueria Autentica

How To Draw A Phasor Diagram For 3 | Taqueria Autentica
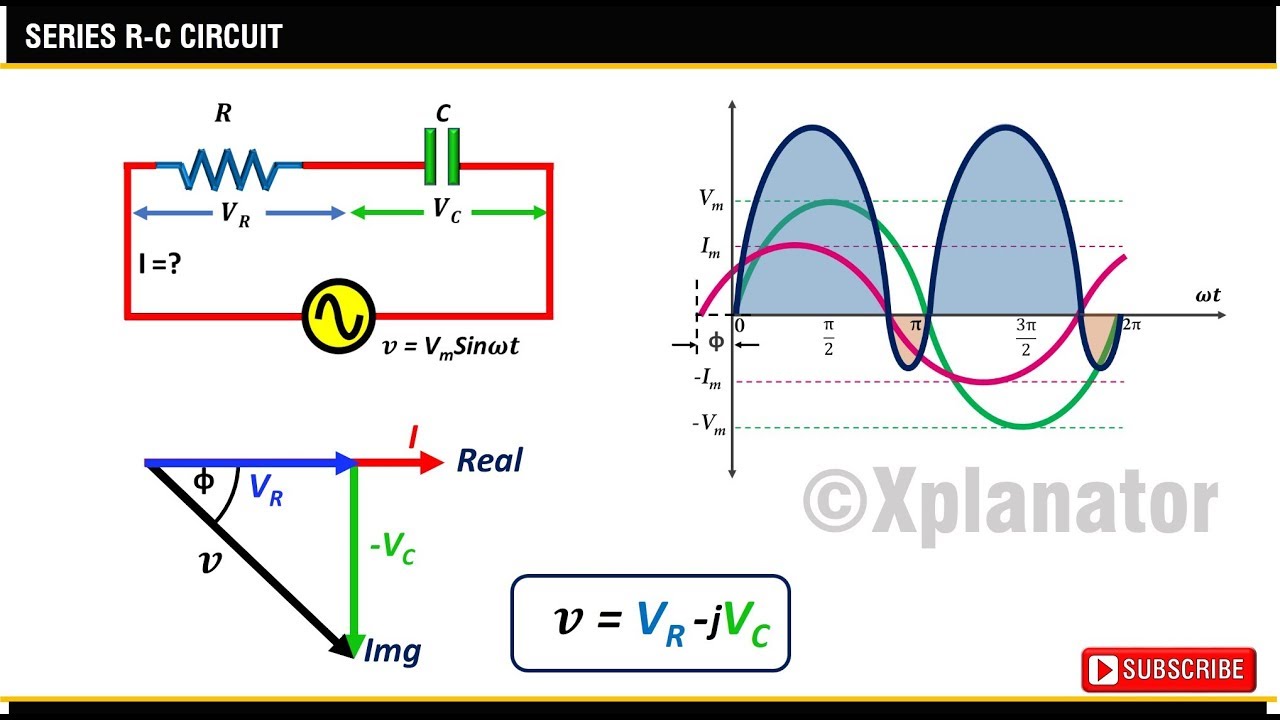
Parallel Rc Circuit Phasor Diagram | Taqueria Autentica

Induction Motor Phasor Diagram | Taqueria Autentica

Phasor Diagrams For Ac Circuits | Taqueria Autentica

Phasor Diagram Of Rl Circuit | Taqueria Autentica