Unlocking Polynomial Arithmetic: Mastering Addition and Subtraction
Ever wondered how seemingly abstract mathematical concepts connect to the real world? Polynomial arithmetic, specifically addition and subtraction, serves as a foundational building block in fields ranging from physics and engineering to computer science and finance. Understanding these operations is key to unlocking a deeper understanding of more complex mathematical ideas.
Polynomial manipulation might sound intimidating, but it’s surprisingly straightforward once you grasp the underlying principles. At its core, adding and subtracting polynomials boils down to combining like terms – terms with the same variable raised to the same power. Think of it like organizing your closet: you group similar items together, like shirts with shirts and pants with pants. Similarly, in polynomial arithmetic, you combine x² terms with x² terms, x terms with x terms, and constant terms with constant terms.
The historical roots of polynomial manipulation can be traced back centuries. Early mathematicians grappled with representing unknown quantities and developing methods for solving equations. Polynomials emerged as a powerful tool for expressing these unknowns and performing calculations, paving the way for advancements in algebra and other mathematical disciplines.
The importance of these operations lies in their wide applicability. They are essential for solving equations, modeling real-world phenomena, and understanding advanced mathematical concepts like calculus and linear algebra. Difficulties with polynomial addition and subtraction can often arise from confusion about combining like terms or dealing with negative coefficients. However, with practice and a clear understanding of the rules, these challenges can be overcome.
A polynomial is an expression consisting of variables and coefficients, combined using addition, subtraction, and multiplication. For example, 3x² + 2x - 5 is a polynomial. Adding polynomials involves combining like terms. For instance, (3x² + 2x - 5) + (x² - x + 2) = 4x² + x - 3. Subtracting polynomials is similar, but remember to distribute the negative sign to all terms in the second polynomial. (3x² + 2x - 5) - (x² - x + 2) = 2x² + 3x - 7.
One benefit of mastering polynomial operations is its application in physics. Polynomials are used to represent physical quantities like displacement, velocity, and acceleration. Another benefit is in computer science, where polynomials are used in algorithms and data structures. In finance, polynomials can model growth and decay of investments.
To solve polynomial addition/subtraction questions, first identify the like terms. Then, add or subtract the coefficients of the like terms. Finally, write the simplified polynomial in standard form, with terms arranged in descending order of exponents.
Checklist: 1. Identify like terms. 2. Add/subtract coefficients. 3. Write in standard form.
Step-by-step guide: 1. Write the polynomials vertically, aligning like terms. 2. Add or subtract the coefficients of each pair of like terms. 3. Write the result in standard form.
Advantages and Disadvantages of Focusing on Polynomial Arithmetic
| Advantages | Disadvantages |
|---|---|
| Foundation for higher-level math | Can seem abstract without real-world context |
| Applicable to various fields | Initial learning curve for some students |
Best Practice: 1. Always identify like terms before performing any operations. 2. Be mindful of the signs when subtracting polynomials. 3. Practice with a variety of examples. 4. Check your work by substituting values for the variables. 5. Seek help if needed.
Real Examples: 1. Calculating the area of a rectangular garden. 2. Determining the trajectory of a projectile. 3. Modeling the growth of a bacterial population. 4. Designing algorithms in computer science. 5. Analyzing financial data.
Challenges and Solutions: 1. Difficulty identifying like terms: Solution - Use color coding or underlining. 2. Mistakes with negative signs: Solution - Distribute the negative sign carefully. 3. Combining unlike terms: Solution - Remember only like terms can be combined.
FAQs: 1. What is a polynomial? 2. How do you add polynomials? 3. How do you subtract polynomials? 4. What are like terms? 5. What is standard form? 6. Why are polynomials important? 7. What are some real-world applications of polynomials? 8. Where can I find more practice problems?
Tips and tricks: Use visual aids like colored pencils to highlight like terms. Practice regularly to build proficiency. Start with simple examples and gradually increase complexity.
In conclusion, mastering polynomial addition and subtraction is crucial for anyone pursuing a STEM field or simply wanting to improve their mathematical skills. These seemingly basic operations form the bedrock of more advanced concepts, enabling us to model and understand the world around us. While the initial learning curve may seem daunting, consistent practice and a focus on the underlying principles will quickly lead to proficiency. Understanding polynomial arithmetic opens doors to a deeper comprehension of mathematics and its powerful applications in diverse fields. By focusing on these core skills, you empower yourself to tackle more complex problems and appreciate the beauty and practicality of mathematics. Embrace the challenge, practice diligently, and unlock the potential of polynomial arithmetic. Explore additional resources online and in textbooks to solidify your understanding and discover even more applications of this essential mathematical tool.

Adding Polynomials Worksheet Answers | Taqueria Autentica

10 Adding Polynomials Worksheet With Answers worksheetocom | Taqueria Autentica

Practice Questions Of Polynomial | Taqueria Autentica
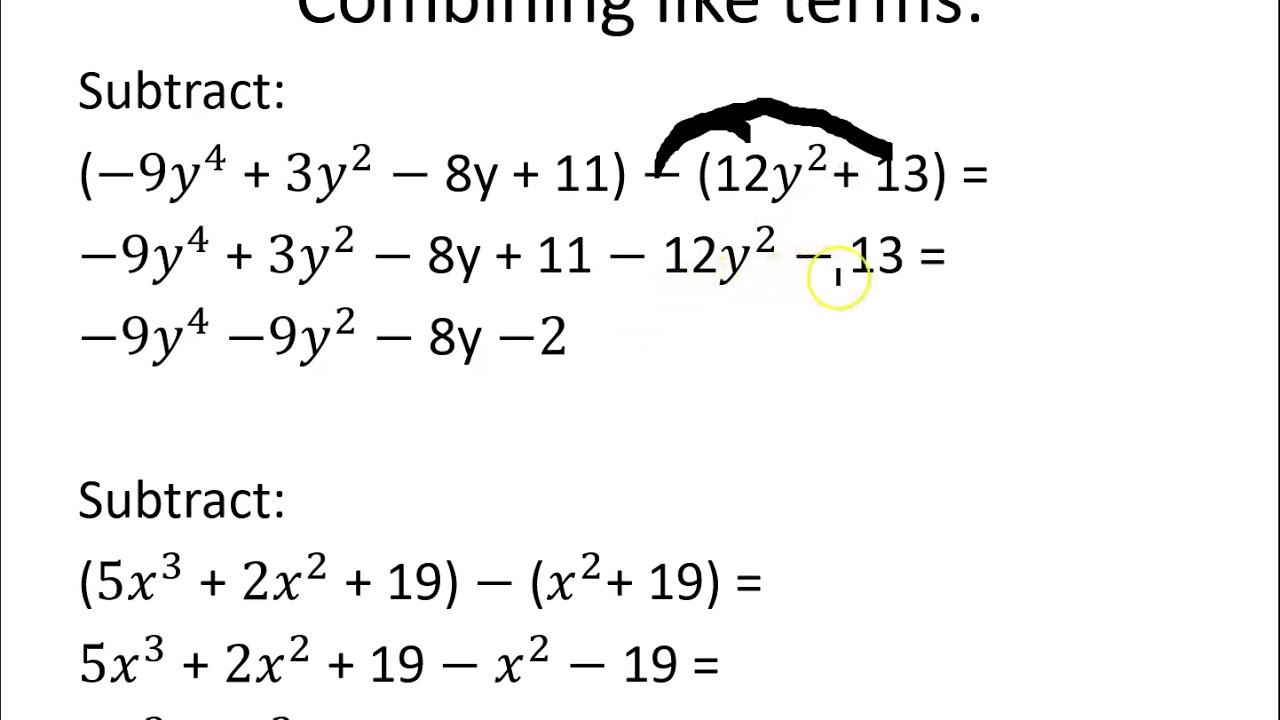
Adding And Subtracting Polynomials Questions | Taqueria Autentica

Adding And Subtracting Polynomials Worksheet | Taqueria Autentica

Adding And Subtracting Polynomials Questions | Taqueria Autentica

adding and subtracting polynomials questions | Taqueria Autentica

Adding and Subtraction Polynomials | Taqueria Autentica

Adding and Subtracting Polynomials Worksheets with Answer Key | Taqueria Autentica

Adding And Subtracting Polynomials Questions | Taqueria Autentica

Adding And Subtracting Polynomials Worksheets With Answer Ke | Taqueria Autentica

Adding And Subtracting Polynomials Worksheet With Answers | Taqueria Autentica

Questions With Multiplying Polynomials | Taqueria Autentica

Adding and Subtracting Polynomials Worksheets with Answer Key | Taqueria Autentica

Adding and subtracting polynomials | Taqueria Autentica