Unlocking Real-World Puzzles with Trigonometry
Imagine needing to find the height of a tall tree without climbing it, or wanting to calculate the distance to a ship at sea. These scenarios might seem impossible, but they become solvable with the power of trigonometry. This branch of mathematics provides us with the tools to tackle real-world problems involving triangles and angles, bridging the gap between theoretical concepts and practical applications.
Trigonometry, meaning "triangle measurement," has a rich history dating back to ancient civilizations. Egyptians used it for surveying land and constructing pyramids, while Greeks explored its applications in astronomy and navigation. The fundamental principles, however, remain relevant today. By understanding the relationships between angles and sides in right triangles, we can decipher unknown distances and dimensions in diverse fields, including engineering, architecture, physics, and even video game design.
At its core, trigonometry revolves around three primary functions: sine (sin), cosine (cos), and tangent (tan). These functions represent ratios between the sides of a right triangle relative to one of its acute angles. For instance, the sine of an angle is the ratio of the length of the side opposite the angle to the length of the hypotenuse. Grasping these fundamental ratios paves the way for unraveling more complex problems.
However, like any problem-solving method, working with trigonometry can present challenges. Accurately visualizing the problem, identifying the correct trigonometric function to employ, and converting between different units of measurement require careful attention. Practice is key to overcoming these hurdles. By working through various examples and focusing on understanding the underlying concepts, we can develop a strong intuition for applying trigonometry effectively.
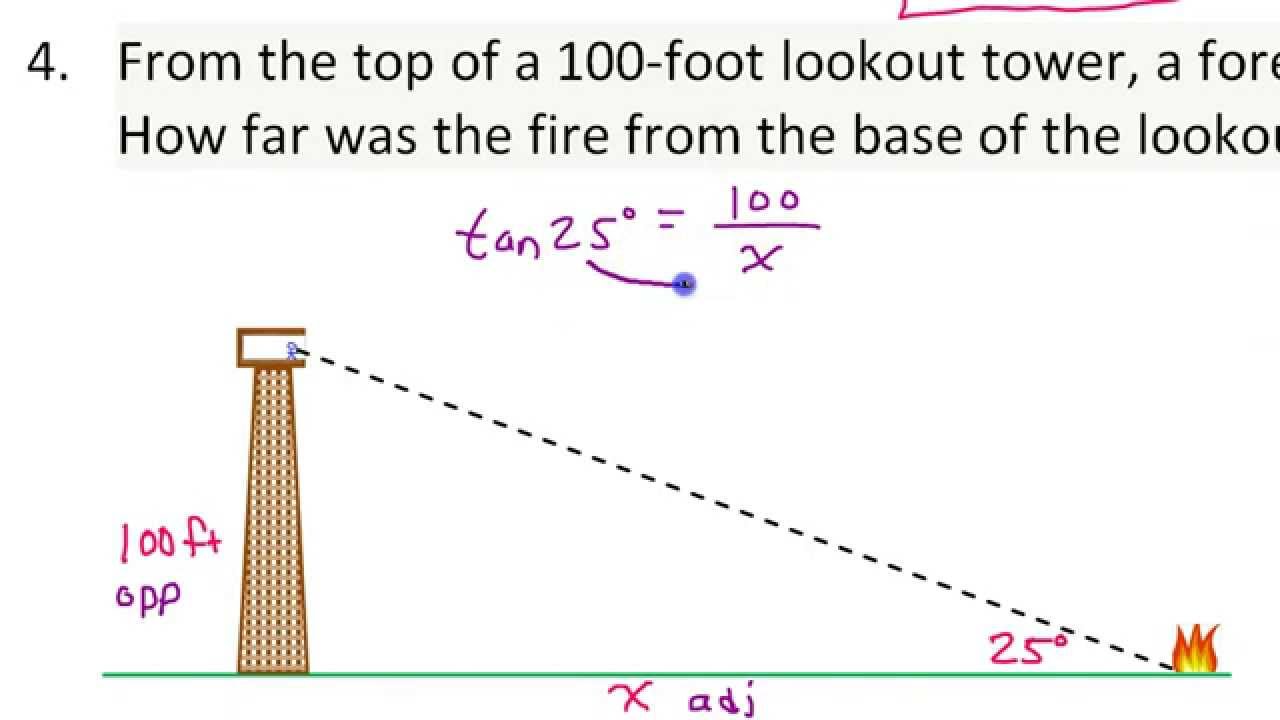
To successfully navigate trigonometric word problems, a systematic approach is essential. Begin by carefully reading and visualizing the problem, identifying what information is given and what needs to be determined. Sketching a diagram can be immensely helpful in visualizing the relationships between the given quantities. Next, identify the appropriate trigonometric function that connects the known and unknown quantities. Once the equation is set up, solve for the unknown variable, ensuring that units are consistent throughout the calculation. Finally, interpret the result in the context of the original problem, checking whether it makes sense and answers the question posed.
Advantages and Disadvantages of Using Trigonometry to Solve Word Problems
While trigonometry provides powerful tools to unlock solutions in various scenarios, it is important to recognize both its strengths and limitations.
| Advantages | Disadvantages |
|---|---|
|
|
To further illustrate the practicality of trigonometry, let's delve into a few examples:
- Finding the Height of a Building: Suppose you want to determine the height of a building. Standing a certain distance away, you measure the angle of elevation to the top of the building. With this angle and the distance from the base of the building, you can use the tangent function to calculate the building's height.
- Navigating at Sea: Sailors rely on trigonometry to navigate the vast ocean. By measuring the angle between the horizon and a celestial object, like the sun or a star, they can determine their latitude. Combined with other navigational techniques, trigonometry becomes an indispensable tool for safe and accurate seafaring.
- Designing Ramps for Accessibility: Architects and engineers use trigonometry to design ramps that meet accessibility standards. By calculating the angle of inclination and the length of the ramp, they ensure safe and comfortable access for individuals with mobility challenges.
While mastering trigonometry for problem-solving takes practice, the rewards are significant. By developing a strong foundation in this fundamental area of mathematics, we equip ourselves with the skills to tackle real-world challenges with confidence and precision.
solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

Question Video: Using Right | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica

solving word problems with trigonometry | Taqueria Autentica