Unveiling the Elegance of Voltage in Phasor Form
Imagine a world where the intricate dance of alternating currents, with their ceaseless ebb and flow, could be captured in a single, elegant mathematical expression. This is the power of representing voltage in phasor form – a transformative concept that has revolutionized our understanding and analysis of AC circuits. It's a doorway to a deeper comprehension of electrical phenomena, allowing us to move beyond the limitations of purely time-domain analysis.
The conventional representation of AC voltage as a sinusoidal function of time, while accurate, can become cumbersome when dealing with complex circuits containing multiple voltage sources and reactive components. Phasor representation offers an ingenious solution by transforming these sinusoidal functions into complex numbers, thereby simplifying calculations and providing a more intuitive grasp of circuit behavior.
This shift in perspective, from the fluctuating realm of time-domain analysis to the static elegance of the phasor domain, is akin to viewing a spinning wheel not as a blur of motion, but as a single, stationary point representing its overall rotation. This concept, rooted in complex number theory, allows us to visualize and manipulate AC quantities with ease, revealing hidden relationships and simplifying complex calculations.
The historical development of phasor representation is intertwined with the growth of our understanding of AC circuits and the mathematical tools needed to analyze them. Charles Proteus Steinmetz, a pioneering electrical engineer, is often credited with popularizing the use of complex numbers in electrical engineering, paving the way for the widespread adoption of phasor analysis. This mathematical innovation proved invaluable in the design and analysis of power systems, enabling engineers to tackle the complexities of alternating current with newfound clarity.
The importance of voltage phasors lies in their ability to simplify AC circuit analysis. By transforming sinusoidal voltages and currents into complex phasors, we can replace differential equations with algebraic equations, making calculations significantly easier. This simplification is especially crucial in circuits with inductors and capacitors, where the phase relationships between voltage and current become critical. The phasor representation elegantly captures these phase relationships, allowing us to analyze circuit behavior in a more intuitive and efficient manner.
A phasor representation of voltage encapsulates both the magnitude and phase of a sinusoidal voltage. It is represented as a complex number, often in polar or rectangular form. The magnitude of the phasor corresponds to the peak value of the sinusoidal voltage, while the angle represents the phase shift relative to a reference waveform. For example, a voltage represented by the phasor 10∠30° signifies a sinusoidal voltage with a peak value of 10 volts and a phase angle of 30 degrees leading the reference.
Benefits of using phasor representation include simplified AC circuit analysis, easier handling of phase relationships, and facilitation of frequency-domain analysis techniques. For instance, impedance calculations, which would involve complex differential equations in the time domain, become simple algebraic operations in the phasor domain.
To work with voltage phasors, one needs to convert time-domain sinusoidal functions to phasor form and vice-versa. This involves identifying the amplitude and phase of the sinusoidal voltage. Standard complex number operations, such as addition, subtraction, multiplication, and division, can then be applied to phasors to analyze circuit behavior. Finally, the phasor result can be converted back to the time domain to obtain the actual sinusoidal voltage waveform.
Advantages and Disadvantages of Voltage in Phasor Form
| Advantages | Disadvantages |
|---|---|
| Simplifies AC circuit analysis | Primarily applicable to steady-state sinusoidal analysis |
| Facilitates frequency-domain analysis | Requires understanding of complex numbers |
| Clearly represents phase relationships | Doesn't directly represent transient behavior |
Frequently Asked Questions about Voltage in Phasor Form:
1. What is a phasor? - A phasor is a complex number representing a sinusoidal function.
2. Why use phasors? - Phasors simplify AC circuit analysis.
3. How to convert a sinusoidal voltage to a phasor? - Identify the amplitude and phase angle of the sinusoidal voltage.
4. How to convert a phasor back to a time-domain waveform? - Use the magnitude and angle of the phasor to construct the sinusoidal function.
5. What are the applications of phasor analysis? - Power systems analysis, circuit design, and control systems.
6. What is the relationship between phasors and impedance? - Impedance is a complex quantity representing the relationship between voltage and current phasors.
7. How do phasors represent phase relationships? - The angle of a phasor represents its phase shift relative to a reference.
8. What are the limitations of phasor analysis? - Phasor analysis is primarily applicable to steady-state sinusoidal signals.
Tips and tricks for working with voltage phasors include using software tools like MATLAB or Python for complex number calculations, visualizing phasors graphically to understand phase relationships, and practicing converting between time-domain and phasor representations.
In conclusion, the representation of voltage in phasor form stands as a testament to the power of mathematical abstraction in simplifying complex physical phenomena. By transforming the dynamic oscillations of AC voltage into static phasor representations, we gain a powerful tool for analyzing and understanding AC circuits. This elegant technique has revolutionized electrical engineering, enabling the design of intricate power systems and advanced electronic devices. As we continue to explore the intricacies of the electrical world, the phasor representation of voltage will undoubtedly remain a cornerstone of our analytical toolkit. Embracing this concept opens doors to a deeper appreciation of the elegant interplay between mathematics and the physical world, empowering us to unravel the mysteries of electricity and harness its potential for the benefit of humankind.

Phasor diagram of voltage and current of system shown in Figure 4 in | Taqueria Autentica

Phasor Diagram For Inductive Circuit | Taqueria Autentica

Basic Phasor Diagram Electric Circuit | Taqueria Autentica

Rectangular to Polar form Polar to Rectangular form conversion | Taqueria Autentica

Phasor Diagram Rlc Circuit Parallel | Taqueria Autentica

The Complete Guide to the Square Root of Three in Power Calculations | Taqueria Autentica

Transformer In Circuit Diagram | Taqueria Autentica

RC Circuit Phasor Diagram | Taqueria Autentica

voltage in phasor form | Taqueria Autentica

Point Voltage Definition at Marlene Ball blog | Taqueria Autentica
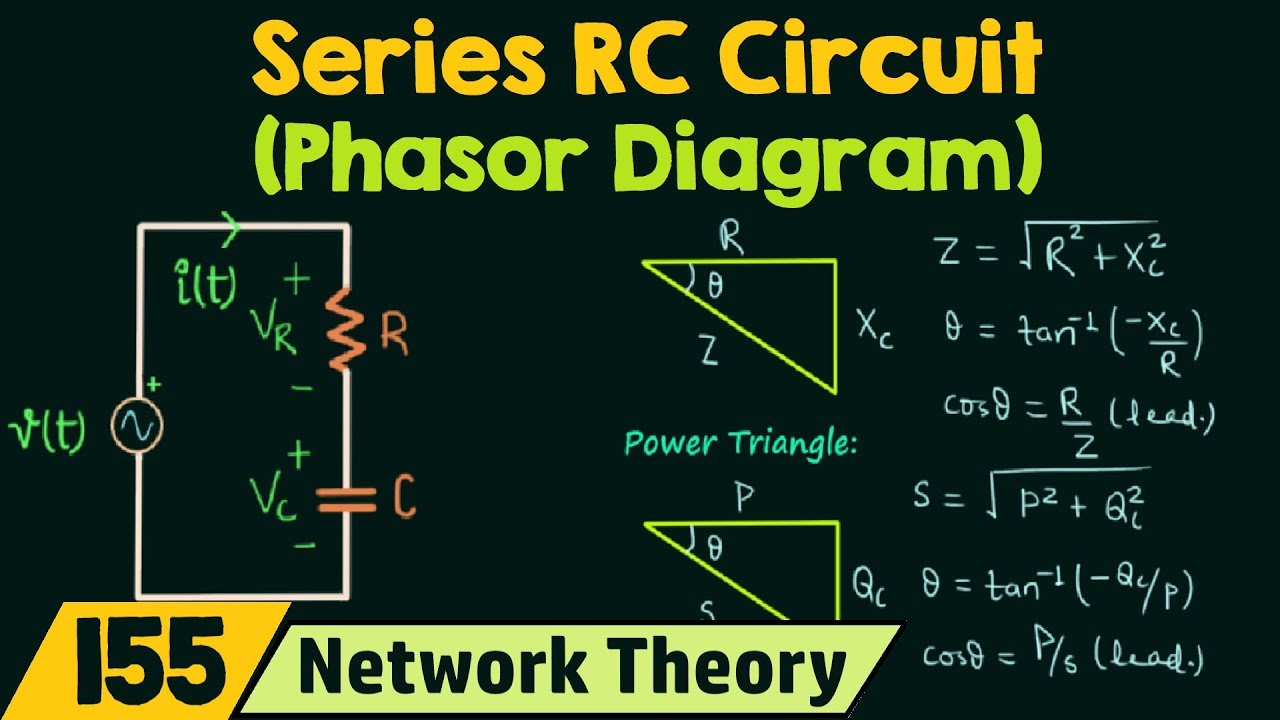
Phasor Diagram Of Rc Series Circuit | Taqueria Autentica

voltage in phasor form | Taqueria Autentica
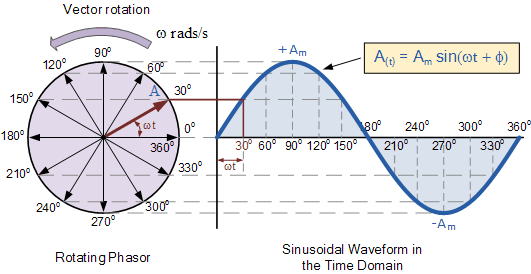
Schneider Electric Phasor Diagram | Taqueria Autentica
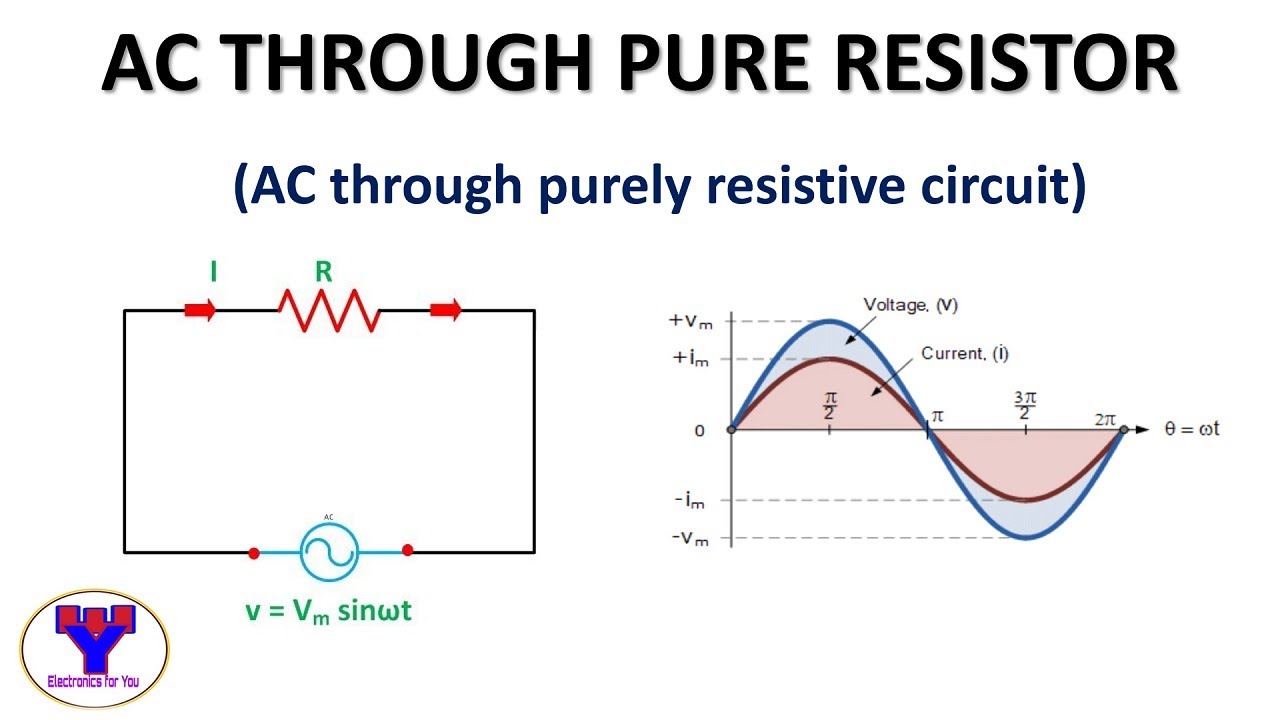
What Does A Purely Resistive Circuit Mean at Felipe Rogers blog | Taqueria Autentica

Current Phasor Diagram Rlc Circuit | Taqueria Autentica